2024年2月15日(木)に実施された第76回診療放射線技師国家試験の放射線物理学の問題を見ていきます。
翌年からフォーマットが変更になるということで、旧フォーマットの最終年です。
少し寂しいような気もしますが、放物の出題内容を確認していきましょう。
AMを見ていきましょう
まずはAM問題から見ていきましょう。
例年70問目からが放物の問題でしたね。
来年以降、どうなることやら。
まぁ、順番はともかく、私としては、毎年学生が解きやすい問題が出題されますように!って願ってます。
AM70
第76回 2024年 AM70
安定な原子核で質量数とおよそ比例関係にあるのはどれか。
- 体 積
- 半 径
- 密 度
- 中性子過剰数
- 核子結合エネルギー
これはいきなりドキッとする問題ですね。
落ち着いて考えれば分かると思いますが、慌てると、ふと誤答枝に食いついてしまいそうです。
解説を見る。
答えは 1 ですね。
原子核の半径と質量数の関係、半径と体積の関係、この2点から導くことができます。
各文字を以下のように定義します。
- r:原子核の半径
- A:原子核の質量数
- V:原子核の体積
- π:円周率
すると、原子核の半径 r と質量数 A の間にはこんな関係がありましたね。
$$r\propto A^{\frac{1}{3}}$$
原子核の半径は質量数の1/3乗に比例します。
なおかつ、原子核は球体構造なので、体積はこう表します。
$$ V=\frac{4}{3} πr^3$$
この2つを組み合わせると、原子核の体積と質量数の関係性が見えてきます。
$$
\begin{aligned}
V&=\frac{4}{3} πr^3\\[6pt]
&=\frac{4}{3} π {(A^{\frac{1}{3}})}^3\\[6pt]
&=\frac{4}{3} πA
\end{aligned}
$$
この式から、原子核の体積は質量数に比例することが分かりますね。
AM71
第76回 2024年 AM71
運動エネルギーが1 GeVの12C原子核を1 nAのビーム強度で30秒間流した。12C原子核によって運ばれた総エネルギー[J]に最も近いのはどれか。
- 1
- 2
- 5
- 10
- 30
炭素ビームの総合エネルギーを問う出題ですね。
1GeVを単純に J 換算しても答えになりませんから、注意してください。
単位を元に立式してみましょう。
解説を見る。
答えは 3 ですね。
文字の定義は以下の通り。
- E:加速粒子1個分のエネルギー
- q:加速粒子の電荷
- e:素電荷量
- V:加速電圧
- I:電流
- t:照射時間
- Et:総エネルギー
また、電流の単位[ A ]は[C/s]に変換できることと、[CV]が[ J ]になることも利用します。
まず、1GeVの炭素線ということから、加速電圧を求めましょう。
$$
\begin{aligned}
E&=\frac{q}{e} V \\[6pt]
1\times 10^9&=\frac{6\times1.6\times10^{-19}}{1.6\times 10^{-19}}V\\[6pt]
V&=\frac{1}{6} \times 10^9 \:\mathrm{[V]}
\end{aligned}
$$
加速電圧が分かれば、エネルギーの J を算出することができます。
$$
\begin{aligned}
E_t&=IVt\\[6pt]
&=1\times10^{-9} \times \frac{1}{6} \times 10^9 \times 30\\[6pt]
&=5\:\mathrm{[ J ]}
\end{aligned}
$$
電流の[ A ]を[C/s]とし、そこに照射時間の[ s ]を乗じることで電荷[ C ]にします。
電荷[ C ]に電圧[ V ]を乗じるとエネルギー[ J ]になることを利用して解いていきます。
AM72
第76回 2024年 AM72
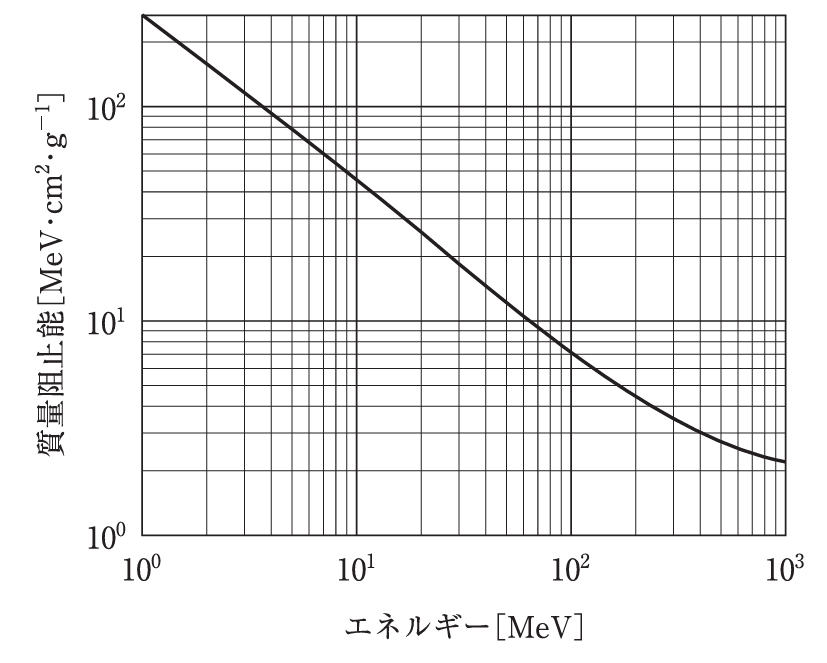
陽子線の水に対する質量阻止能とエネルギーとの関係を図に示す。
10 MeV重陽子線の水に対する質量阻止能[MeV・cm2・g-1]に最も近いのはどれか。
- 20
- 30
- 50
- 80
- 100
この問題、難問です。
想定の解き方から外れると、ドツボにハマることになります。
解説を見る。
答えは 4 です。
この問題、私としては、4 or 5 の複数解だと思っていました。
しかし、考え方のアプローチを変えると、正解の 4 にたどり着きます。
では考え方を見ていきましょう。
最初に誤った解法をご紹介します。
この落とし穴にはまる方、いるんじゃないでしょうか?
まず、グラフから陽子線の質量阻止能を読み取ります。

10MeVの陽子線の質量阻止能は45MeV・cm2・g-1と読み取れます。
質量阻止能(厳密には質量衝突阻止能)は下記の式に比例します。
$$
(\frac{S}{ρ})_{col}\propto \frac{m {z_i}^2}{E} \propto \frac{{z_i}^2}{v^2}
$$
この式を覚えていますか?
各文字の定義はこちら。
- (S/ρ)col 質量衝突阻止能
- m 粒子の質量
- zi 粒子の電荷数
- E 粒子のエネルギー
- v 粒子の速度
陽子線と重陽子線の阻止能比を把握しましょう。
$$
\color{#B22222}{
\begin{aligned}
(\frac{S_p}{ρ})_{col}&\propto \frac{m {z_i}^2}{E} \\[6pt]
&= \frac{1 \cdot {1}^2}{E}\\[6pt]
&=\frac{1}{E}
\end{aligned}
}$$
$$
\color{MidnightBlue}{
\begin{aligned}
(\frac{S_d}{ρ})_{col}&\propto \frac{m {z_i}^2}{E} \\[6pt]
&= \frac{2 \cdot {1}^2}{E}\\[6pt]
&=\frac{2}{E}
\end{aligned}
}$$
$$
\color{MidnightBlue}{(\frac{S_d}{ρ})_{col}}=\color{#B22222}{2(\frac{S_p}{ρ})_{col}}
$$
重陽子の質量阻止能(青い文字)は陽子(赤い文字)の2倍であることが分かります。
グラフから読み取った値を2倍すると、10MeVの重陽子線の質量阻止能は約90MeV・cm2・g-1と求められます。
したがって選択肢は90の・・・・・・ない!?
そうなんです。選択肢に90がないんです。
80?100??
何度グラフを見てみても、陽子線の質量阻止能は45MeV・cm2・g-1と読み取れます。
近しい値にしようとも、80も100も同じだけ離れています。
ナニコレ?
この方法はダメということですね。
では、正解が導けるアプロ―チをご紹介。
※ここから先が、正解にたどり着くための考え方です。
最初に陽子線と重陽子線の阻止能比を把握します。
先ほどのとおり、重陽子線の質量阻止能は陽子線の2倍です。
ということは、10MeVの陽子線と同じ質量阻止能を得るのに、重陽子線は5MeVでOKと考えることもできます。
グラフを読み取ってみましょう。

この方法なら80MeV・cm2・g-1と読み取ることができます。
ちょっと意地悪な問題でしたね。
二度と出題して欲しくないと思います。
こういう回答が割れる可能性がある問題は国家試験の問題としては相応しくないと思います。
誰もが知っている・思いつく解法で正解が導ける問題が良いと思うのですが、どうでしょうか?
わざわざ受験生に頭を抱えさせなくても良いんじゃないでしょうか・・・
気を取り直して、次!
AM73
第76回 2024年 AM73
電磁波で正しいのはどれか。2つ選べ。
- 縦波である。
- 電荷を有する。
- 波長が短いほどエネルギーは大きい。
- 伝播速度は波長と周波数の積に等しい。
- 周波数は紫外線よりマイクロ波の方が高い。
幾度となく出題されるパターンですね。
これは必ず得点しなきゃならない問題ですね。
解説を見る。
答は 3と4 です。
- 誤り。電磁波(X線やガンマ線)は横波でしたね。縦波は超音波です。
- 誤り。電磁波は電荷を有しません。したがって、電場や磁場中で直進するんでしたね。
- 正解。電磁波のエネルギーEは振動数をν、波長をλ、プランク定数をh、速度をcとすると以下(選択枝5のあと)のように表します。
- 正解。速度c、波長λ、振動νには以下の関係性があります(択枝5のあと)。単位を添えて考えるとわかりやすいかと思います。
- 誤り。周波数は紫外線の方が高いですね。マイクロ波が1mm程度、紫外線が100~400nm程度です。
$$
E=hν=\frac{hc}{λ}
$$
$$
\begin{aligned}
c &=λ \nu \\[6pt]
\mathrm{[\frac{m}{s}]} & =\mathrm{[m]}\,\mathrm{[\frac{1}{s}]}
\end{aligned}
$$
AM74
第76回 2024年 AM74
LETで正しいのはどれか。
- 単位はm-1である。
- 荷電粒子の電荷の2乗に反比例する。
- 荷電粒子の運動エネルギーに比例する。
- カットオフエネルギーが無限大のとき線衝突阻止能と同義である。
- 単位質量あたりに付与する全エネルギーが同じときLETは等しい。
解説を見る。
答えは 4 です。
- 誤り。LETの単位は J/m です。
- 誤り。LETは線エネルギー付与と言いますが、別名は限定線衝突阻止能です。したがって、阻止能が電荷の2条に比例することから、LETも電荷の2条に比例します。質量衝突阻止能の関係式を後に示します。質量阻止能は線阻止能を密度で除したもので、電荷やエネルギーの比例関係に変化はない。
- 誤り。2同様、運動エネルギーは反比例の関係にある。
- 正解。記載です。覚えましょう。線衝突阻止能のエネルギー範囲を限定的にしたものがLETです。そのエネルギー制限を開放し無限大にすれば、線衝突阻止能と同義になります。
- 誤り。「単位長さ当たり」である。
$$
(\frac{S}{ρ})_{col}\propto \frac{m {Z_i}^2}{E} \propto \frac{{Z_i}^2}{v^2}
$$
- (S/ρ)col 質量衝突阻止能
- m 粒子の質量
- zi 粒子の電荷数
- E 粒子のエネルギー
- v 粒子の速度
PMも見ていきましょう
AMは難しいのが1問ありましたね。
気を取り直して、午後の問題も見ていきましょう。
PM70
第76回 2024年 PM70
基底状態にある Sr 原子の最外殻の軌道電子配置はどれか。
- 4s2
- 4s24p4
- 5s2
- 5s25p2
- 6s1
電子配置の問題ですね。
これ、苦手な方、結構多いんじゃないでしょうか?
一度覚えてしまえば、簡単にできるようになりますから、覚悟を決めて覚えちゃいましょう。
解説を見る。
答えは 3 です。
まずはSrの原子番号を確認しましょう。

Srの原子番号は38番です。
したがって、軌道電子の数も38個となります。
では、その38個の軌道電子がどのように配列されるのか考えていきます。
それぞれの電子軌道に入る電子数を確認しておきましょう。
K殻には1s軌道があり、2個の軌道電子が入ります。
L殻には2s軌道と2p軌道があり、2s軌道に2個、2p軌道に6個でL殻全体としては8個の軌道電子が入ります。
M殻には3s軌道、3p軌道、3d軌道があり、3s軌道に2個、3p軌道に6個、3d軌道に10個でM殻全体としては18個の軌道電子が入ります。
N殻には・・・キリがないので表にまとめます。

これで各軌道にいくつの軌道電子が配置されるかは分かりました。
今回必要になるのはもう一つ外側のO殻までです。
表の続きを書いてみましょう。
そして、もう一つ把握しておかなければならないのが、配置の順番です。

1番の矢印から順を追って見ていきます。
まずは1番矢印。
1s軌道に2つ配置されます。
次いで2番矢印。
2s軌道に2つ。
ここまでで4個の軌道電子が配置されました。
原子番号4番までですね。
続けます。
3番矢印行きます。
2p軌道に6つ。
3s軌道に2つ。
ここまでで10個の軌道電子が配置されています。原子番号10番まで。
4番矢印で変化が生じます。
ここまではK殻→L殻→M殻とすべてきれいに埋まってから外側の軌道に移ってきましたが、3pと3dの間で単純な規則性は破綻します。
見ていきます。
3p軌道に6つ。
3dに行きたいところですが、先に4sに2つ。
そして5番矢印の3dに10個配置されます。
4pに6つ。そして3dのときと同様に先に5s。
5sに2つ入ったところで、38個の軌道電子が配置されたことになります。
模式図的にSrの電子配置を図示してみましょう。

最外殻には31番目と32番目に配置された2つの軌道電子が存在します。
O殻(主量子数が5)のs軌道に2つ配置されているので、 5s2 となります。
どうでしょうか?やり方を覚えれば解けそうな気になってきませんか?
PM71
第76回 2024年 PM71
60 keV 光子の水中における前相互作用数に対するコンプトン効果の寄与の割合[ % ]に最も近いのはどれか。
- 25
- 40
- 55
- 70
- 85
これはAM72に引き続き、難問ですね。
どちらかといえば、こちらの方が難しいかもしれないです・・・
解説を見る。
答は 5 です。
コンプトン効果の寄与率に関する問題ですね。
光子のエネルギーによって主に生じる相互作用は変化していきます。
図を参照してください。

物質が水の場合、30keV~30MeVの範囲では主にコンプトン効果が起こることが分かります。
60keVの光子の場合もコンプトンが主といえます。
そうしますと、選択肢は 3 or 4 or 5 となります。
私は最初、ここから先の判断に迷ってしまいました。
光子エネルギーと質量減弱係数の関係を示したグラフを参考にしようと、教科書や参考書の類を色々と探しました。
鉛やアルミニウムのグラフは見つかったものの、水のグラフがなかなか見つからなかったからです。
選択肢に50%以上のものを1つにするか、エネルギーを1MeVにしていただかないと、選びきれないと思いました。
で、過去問を漁ってみたところ、ありました。
第74回 PM72
https://www.mhlw.go.jp/seisakunitsuite/bunya/kenkou_iryou/iryou/topics/dl/tp220421-06b_01.pdf 厚生労働省HPより
このグラフから60keVの質量減弱係数を参考にコンプトン効果の寄与率を検証していきます(オレンジ線)。
![光子エネルギー(keV)に対する水の質量減弱係数のグラフ。
縦軸は質量減弱係数 [cm²/g]、横軸は光子エネルギー [keV](対数軸)。
・黒実線:全質量減弱係数
・青破線:コンプトン効果
・緑点線:光電効果
・赤点線:干渉性散乱(コヒーレント散乱)
・オレンジ線:60 keVの位置を示す補助線あり。
60 keV付近ではコンプトン効果が全体に最も大きく寄与している。](https://houbutsu.net/wp-content/uploads/2025/04/第76回 PM71 水の質量減弱係数-1024x895.png)
コンプトン効果に比べて、光電効果や干渉性散乱の寄与は極僅かであることが読み取れます。
したがって、コンプトン効果の寄与率は85%の選択枝 5 が妥当だと判断できます。
過去問として出題されたグラフが参考になるなんて・・・
やっぱり過去問で勉強するのが良さそうですね。
PM72
第76回 2024年 PM72
中性子の性質で正しいのはどれか。
- 自由空間中ではβ+壊変する。
- 静止質量は陽子と電子の静止質量の和よりも大きい。
- 熱中性子の室温でのエネルギーの最確値は 0.25 eV である。
- 熱中性子の捕獲反応断面積は中性子の運動エネルギーに反比例する。
- 速中性子が重陽子と弾性散乱したときに失う運動エネルギーの最大値は散乱前の運動エネルギーに等しい。
解説を見る。
答えは 2 です。
- 誤り。自由中性子はβ–壊変する。β+壊変は陽子が中性子に代わる壊変。
- 正解。陽子の質量は電子の1836倍、中性子の質量は電子の1839倍。したがって、正しい枝である。
- 誤り。熱中性子のエネルギーの最確値(最頻値)は 0.025eV 、速度に換算すると 2200m/s である。小数点の位置もしくは単位の接頭語でひっかけてくる王道のパターンですね。こちらとしては学生にここで引っ掛からせるわけにはいきません。
- 誤り。熱中性子の捕獲断面積は速度に反比例する。これを1/v法則といいます。エネルギーの場合はエネルギーの平方根に反比例する。
- 誤り。散乱前の8/9に相当する。以下の式を参照してください。
$$
\color{#B22222}{
E_R=E_n \cdot \frac{4A}{(A+1)^2} \cdot cos^2θ
}$$
各文字の定義はこちら
- ER:反跳原子核の運動エネルギー(入射中性子の失うエネルギー)
- En:入射中性子の運動エネルギー
- A:標的核(今は重陽子)の質量(質量数で代用して考える)
- cosθ:入射中性子の散乱角
失うエネルギーが最大になるということは、ERが最も大きくなるように計算すれば良いということ。
Aに重陽子の質量数の2を代入。
散乱角は180度。
これで計算すると、
$$
\color{#B22222}{
\begin{aligned}
E_R&=E_n \cdot \frac{4A}{(A+1)^2} \cdot cos^2θ\\[6pt]
&=E_n \cdot \frac{4 \times 2}{(2+1)^2} \cdot cos^2 180 \\[6pt]
&=\frac{8}{9} E_n
\end{aligned}
}$$
今年の問題の中では比較的スムーズに解けましたね。
PM73
第76回 2024年 PM73
X線の発生で正しいのはどれか。2つ選べ。
- 特性X線のエネルギーは管電圧に比例する。
- 制動X線の全強度は管電圧を2倍にすると4倍になる。
- Kα線のエネルギーはモリブデンよりタングステンの方が大きい。
- ターゲットの原子番号が大きくなるほど制動X線の最大エネルギーは大きくなる。
- K特性X線は、ターゲットへの入射電子エネルギーがK殻軌道電子の結合エネルギーより小さいときに生じる。
解説を見る。
答えは 2と3 です。
- 誤り。特性X線のエネルギーは核種によって固定値であるため、管電圧には左右されない。
- 正解。制動X線の全強度は管電圧の2乗に比例します。したがって、管電圧を2倍にすれば、全強度は22倍で4倍になります。
- 正解。モリブデンのKα線のエネルギーは 17.5keV、タングステンのKα線のエネルギーは59keVです。
- 誤り。制動X線の最大エネルギーは管電圧のみで決まります。
- 誤り。逆ですね。K特性X線は、軌道電子がK殻に遷移してくる際に放出する特性X線である。つまり、K殻に空位を生じさせる必要がある。そのためにはK殻軌道電子を電離することが条件になる。したがって、入射電子のエネルギーはK殻結合エネルギーより大きくなければならない。
PM74
第76回 2024年 PM74
核融合反応
D + T → 4He + n
による核反応のQ値[MeV]に最も近いのはどれか。
ただし、それぞれの粒子の静止質量を
D は 2.014 Da、
T は 3.016 Da、
4He は 4.002 Da、
n は 1.009 Da とし、
統一原子質量単位 1 Da = 930 MeV とする。
- -18
- -5
- 0
- 5
- 18
解説を見る。
答えは 5 です。
これは核融合の内容ですが、統一原子質量単位を使ったよく出題されるパターンですね。
統一原子質量単位で計算し、それをエネルギーに換算するという流れで簡単に解くことができます。
$$
\begin{aligned}
{}^{2}_{1}\mathrm{D}+{}^{3}_{1}\mathrm{T}&→{}^{4}_{2}\mathrm{α}+{}^{1}_{0}\mathrm{n}+Q\\[6pt]
2.014+3.016&=4.002+1.009+Q\\[6pt]
Q&=(5.030-5.011) \times 930\\[6pt]
&=0.019 \times 930\\[6pt]
&=17.67\:\mathrm{[MeV]}
\end{aligned}
$$
いかがですか?
小数点以下の桁を間違えなければ、比較的簡単な計算問題です。
これ、桁数多くて嫌なんや!


まぁまぁ。
原子質量単位の計算は鉄板だから。
第76回 放物 総評
いかがだったでしょうか。
今年は結構難易度の高い出題が目立ちましたね。
出題されているテーマ自体はよく見かけるものでしたが、選択肢に泣かされました。
次年度以降はもう少し選びやすい選択肢になると良いですね。
それと、CT、MRI、超音波といった医療物理の出題がありませんでしたね。
こういう年もあるんですね。
珍しい回だったと思います。
まとめ
この記事では、第76回放射線物理の出題全体を振り返り、難易度や出題傾向について整理しました。
改めてポイントを振り返って、今後の学習につなげていきましょう。
- 今年は難易度の高い設問が比較的多い回だった
- 出題テーマ自体は定番だが、選択肢で判断を迷わせる問題が目立った
- 計算・グラフ読解・概念理解を横断的に要求される設問構成だった
- 一方で、CT・MRI・超音波といった医療物理分野の出題は見られなかった
- 年による出題の偏りを前提に、基礎を広く押さえる学習の重要性を再確認できる回だった

難しかったですね。でも、だからこそ「基礎をちゃんと理解しているか」が試された回だったと思います。
来年に向けて、焦らず一つずつ積み上げていきましょう。

来年の放物は何問目からなんじゃろうかのぉ。
お願い
本サイトに掲載されている図やイラストの著作権は管理人にあります。
無断掲載や転載はお断りさせていただきます。
また、リンクフリーではありますが、画像などへの直リンクはお控えください。
最新国試へのジャンプ

次に読むならコレ!電爺的おすすめ内部リンク

ほれ、ここまで読んだんなら、次はこのあたりを見ておくとえぇぞい。
次に読むならコレ!たまのすけおすすめ外部リンク

ここまで読んできた皆さんなら、もう一歩踏み込んだ知識に触れてみたくなるはずです。そんな方におすすめの外部リンクを紹介しますね。




コメント