「スピン角運動量」や「軌道角運動量」という言葉は聞いたことがあっても、実際にどれが何を指すのかごちゃごちゃしやすいところですよね。
学生さんからもとっても質問の多いジャンルです。
そして、私も実は苦手な分野・・・
それはさておき、この記事では、角運動量の種類と、それぞれに対応する量子数の意味を整理していきます。
核子である陽子や中性子は原子核の中で自転と公転をしています。
自転はスピン角運動量、公転は軌道角運動量と区別できることを確認し、それぞれにどんな量子数が対応するのかを見ていきましょう。
これらの基礎を理解しておくことで、次のステップである「核スピン(全角運動量)」にもスムーズにつながります。
角運動量とは何か?
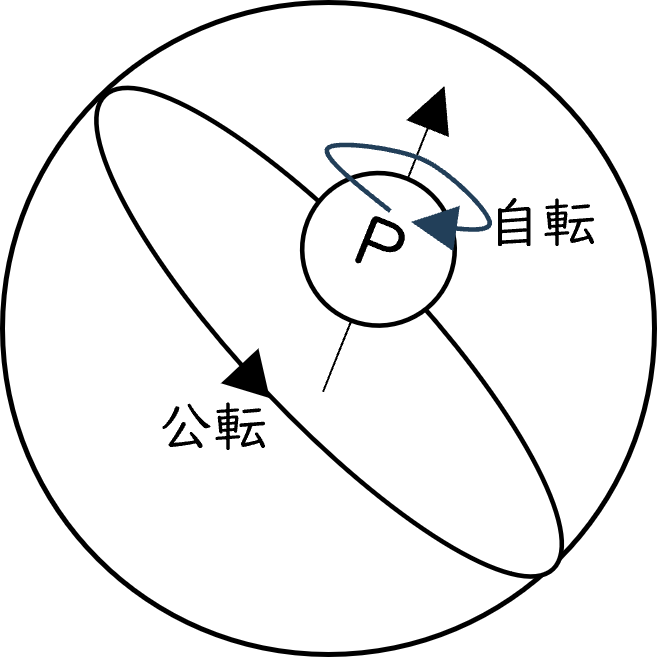
私たちが「回る」と表現する運動には、いくつかの種類があります。
日常ではコマの回転や地球の動きでイメージできますが、原子核の中にも同じように「回る性質」が存在します。
これを物理の世界では角運動量と呼び、原子核や素粒子を理解するうえで欠かせない基本的な概念です。
回転運動と公転運動のちがい
物体が「回る」といっても、その様子には大きく2種類があります。
ひとつは「自分自身が軸を中心に回転する」自転です。
もうひとつは「あるものを中心として、そのまわりを回る」公転です。
地球を例にすれば、1日に1回の自転と、1年かけて太陽のまわりを回る公転がわかりやすいでしょう。
原子核の中でも、陽子や中性子は「粒子としての自転」と「軌道としての公転」を同時に持っています。
これらの“回る動き”が持つ物理量をまとめて「角運動量」と呼びます。
角運動量が意味するもの
角運動量は、簡単にいえば「回転の勢い」を表す量です。
力学で学ぶ運動量が「まっすぐ進む勢い」だとすると、角運動量は「回る動きの勢い」といえます。
角運動量には大きく2種類があります。
粒子そのものが持つ自転に対応するスピン角運動量と、粒子が軌道上を運動(公転)することに対応する軌道角運動量です。
これらは別々に考えられるだけでなく、後で合成して「全体の角運動量」として扱うこともできます。
原子核物理や量子力学では、この角運動量を正しく理解しておかないと、次に登場する「核スピン」の概念にまったくつながりません。
そして、角運動量に伴って磁気モーメントが生じます(特にスピンの場合は大きく関係)。

まずは、「粒子には回転の勢いがある」という直感的なところから押さえていこう。
角運動量の種類を整理しよう
角運動量と一口にいっても、その中身は一種類ではありません。
粒子が自分自身で回転しているのか、それともある軌道を動き回っているのかによって性質が異なります。
ここを整理しておかないと、あとで出てくる量子数との対応関係で混乱してしまいます。
スピン角運動量(自転の量子数)
まず押さえたいのが、粒子そのものが持つ自転の性質です。
陽子や中性子などの核子は、まるで小さなコマのように自分自身の軸を中心に回転しており、この回転がつくる角運動量をスピン角運動量と呼びます。
スピンは量子力学的な性質で、目に見えるような「本当に回っている動き」ではありませんが、便宜的に「粒子が自転している」と考えるとイメージしやすいでしょう。
核子のスピンは常に 1/2 という値を持ち、この特徴が後で核スピンの扱いに深く関わってきます。
つまり、スピン量子数は 1/2 ということになります。
1/2ってメッチャ大事そうやな。
スピン角運動量は内部スピンとも言うらいいで。

軌道角運動量(公転の量子数)
次に考えるのが、核子が核の内部で動き回る運動です。
粒子は単純に止まっているのではなく、互いに力を及ぼし合いながら軌道を描くように運動しています。
このときに生じるのが軌道角運動量です。
軌道角運動量は整数値をとり、0、1、2…と順に割り当てられていきます。
つまり、方位量子数が 0、1、2… ということになります。
これらの数値は「どのくらい複雑な軌道で動いているのか」を示すもので、軌道が複雑になるほど角運動量も大きくなります。
電子の原子軌道で「s軌道」「p軌道」といった区別があるのと同じ考え方で、核の中でも同様に軌道角運動量が量子数で整理されていきます。
電子の軌道量子数と同じ考え方なんですね

電子の量子数はA22:量子数とは?4種類の意味とパウリの排他原理でどうぞ。

量子数で表される角運動量
角運動量の大きさや向きを、私たちは「量子数」という数字で整理して表します。
量子数は、単に記号を並べただけのものではなく、粒子の性質を決める非常に重要な「番号」のような役割を果たしています。
ここでは、角運動量に関わる基本的なルールを確認していきましょう。
整数・半整数というルール
まず押さえておきたいのが、角運動量を表す量子数は「整数」か「半整数」の値しか取らないという点です。
- 軌道角運動量に対応する量子数($l$)は 0、1、2、… といった整数値をとります。
- スピン角運動量に対応する量子数($s$)は $\pmb{\frac{ 1 }{ 2 }}$、$\pmb{\frac{ 3 }{ 2 }}$、$\pmb{\frac{ 5 }{ 2 }}$ 、… といった半整数値をとります。
この違いが、粒子の分類を大きく二つに分けます。
スピンが整数の粒子をボース粒子、半整数の粒子をフェルミ粒子と呼びます。
陽子や中性子、電子はすべてスピン1/2のフェルミ粒子です。
角運動量には「向き」に対応する量子数も存在しますが、ここでは大きさを決めるルールに注目して整理しておけば十分です。
核スピンを学ぶ前に押さえておきたいこと
角運動量と量子数の関係そのものが国家試験に出題されることはほとんどありません。
しかし、この知識は次に学ぶ「核スピン」を理解するための大切な土台になります。
核スピンは、核子が持つスピン角運動量や軌道角運動量を組み合わせて成り立つものです。
だからこそ、それぞれがどんな値をとるのかを整理しておくと、後の理解がスムーズになります。
角運動量の値のルール
角運動量に対応する量子数には、整数か半整数というルールがあります。
- スピン角運動量:常に半整数(陽子・中性子は $\frac{1}{2}$ )
- 軌道角運動量:整数(0、1、2、…)
この区別を押さえておけば、核スピンの仕組みを学ぶときに混乱せず理解できるようになります。
角運動量とスピンのまとめ
磁力の大きさとその向きを表すベクトル量を磁気モーメントといいます。
陽子は電子と同じ電荷を有するので、電子と同じ磁気モーメントを持ちます。
中性子は電荷をもたない粒子ですが、中性子を構成するクォークは電荷を有しているため、弱い磁気モーメントを持ちます。
核子それぞれのスピン角運動量を内部スピンといい、
原子核全体の全角運動量を核スピンといいます。
核スピンは、個々の核子のスピン角運動量と軌道角運動量のベクトル和になります。
実際に出題された国試問題を見てみよう
ちょっと出題年も追えないくらい古い出題ですがご紹介します。
出題年不明
中性子について正しいのはどれか。
- 速中性子の遮へいには鉛が有効である。
- ${}^{238}\mathrm{U}$は熱中性子を捕獲して核分裂を起こす。
- 質量阻止能は陽子と同じである。
- 核スピン量子数は0である。
- 熱中性子の速度は約 2 km/s が多い。
実は、A26記事で紹介する「核スピン」は稀に出題されますが、このA25記事で主に扱った量子数の問題は本当に少ないのです。
主な出題テーマは「中性子」に関するものですが、4番目の枝で「核スピン量子数」が登場しました。
解答を確認する。
正解は 5 です。
- × 速中性子の遮へいは、まず水・ポリエチレンなど水素を多く含む物質で減速させるのが有効。鉛は主にγ線遮へい向きで、中性子遮へい材としては不適。
- × U-238は熱中性子では核分裂しない(非核分裂性)。熱中性子を捕獲すると U-239 → Np-239 → Pu-239 とβ崩壊していく(増殖用の母核=可換核)。核分裂するのは熱中性子に対しては U-235。
- × 中性子は電荷をもたないので、電離損失による質量阻止能という概念は適用しにくい。減速・吸収は主に弾性散乱や捕獲で起こる。
- × 中性子(核子)の内部スピン=1/2。したがって「核スピン量子数は0」は誤り。
※ここで言う“核スピン量子数”という言い回しは古い表現で、粒子自身のスピン量子数 s = 1/2 を指すと考えてよい。 - ◯ 熱中性子の代表速度は約 2.2 km/s(= 2200 m/s)。「約2 km/s」は許容範囲で正しい。

最近の国試では「角運動量」よりも核スピンや熱中性子の性質の方が問われやすいです。
今回の④のような「量子数」の言い回しは古い問題に見られる表現だね。
医療現場でこの知識がどう役立つの?

角運動量や量子数といった話は、一見すると物理の抽象的な世界に思えるかもしれません。
しかし実際には、医療現場で重要な技術につながっています。
代表例が MRI(磁気共鳴画像) です。
MRIでは水素原子核の「核スピン」を利用しています。
核スピンは角運動量の一種であり、これが磁場と相互作用することで信号を取り出すことができます。
逆に言えば、核スピンが 0 の核種では信号が得られないため、MRIでは観測対象になりません。
このように「角運動量」という抽象的な物理概念は、一見関係なさそうに見えても最終的には 医療画像の基盤 に直結しているのです。
次のA26:原子核の全角運動量(核スピン)を理解しようでは、この「核スピン」についてさらに掘り下げていきます。
まとめ
角運動量は「回転の勢い」を表す量であり、粒子が持つスピン角運動量と、運動に対応する軌道角運動量の2つに分けられます。
特に陽子や中性子は常に 1/2 のスピンを持ち、この性質が次に学ぶ核スピンの理解につながっていきます。
一見すると抽象的な量ですが、この考え方を押さえておかないと、核磁気共鳴(MRI)の基礎はつかめません。
「整数か半整数か」というルールの違いを整理して覚えておくことで、試験でも実際の医療現場でも役立つ知識になります。

粒子の回転の勢いが「角運動量」。
この考え方を土台にして、次は核スピンを学んでいこう!
次に読むならコレ!電爺的おすすめ内部リンク

ほれ、ここまで読んだんなら、次はこのあたりを見ておくとえぇぞい。
もっと知りたい方へ!たまのすけおすすめ外部リンク

ここまで読んできた皆さんなら、もう一歩踏み込んだ知識に触れてみたくなるはずです。そんな方におすすめの外部リンクを紹介しますね。



コメント