こんにちは。たなまるです。
磁場の中に入った荷電粒子が、なぜ直進せずに円を描くように動くのか。
「ローレンツ力がはたらくから」と聞いても、
いまいちピンとこない！
イメージしづらい！ ……そんな方いませんか？
ここでは、ローレンツ力の働き方と、
それがどうして円運動を生み出すのかを見ていきます。
力の向き・速度・運動の変化を一つずつ整理しながら、
荷電粒子の動きが自然に理解できるように進めていきます。
物理がちょっと苦手な方でも、
順を追って学べば、磁場中の運動がしっかり頭に入ってくるはずです。
一緒にローレンツ力のイメージをクリアにしていきましょう。
電流がつくる磁界の向きをつかもう
電流が流れると、その周りには必ず磁界ができます。
しかもこの磁界は、ただできるだけではなく、
決まった向きに回り込むという大事な性質があります。
まずは、その回り方のルールをしっかりつかんでいきましょう。
アンペール右ねじの法則とは？
磁界の回り方は、アンペール右ねじの法則 で決まります。
まずは、この法則をイメージして下さい。
右手の親指を電流の向きに伸ばすと、
自然に曲がる4本の指が“磁場が回り込む方向”を示しています。
つまり、
電流の進む方向に対して、右回りに磁界が発生する。
この一文がとても大切なポイントです。
（※「磁場」が発生する。という表現もあります。）
右ねじの法則をほかの図でも確認してみましょう。
次の図は、電流の向きと、その周りにできる磁場の向きを具体的に描いたものです。
図では電流が上向きに流れています。
右ねじを上へ進める時の動きを思い浮かべると、手の指が右方向へ回り込みますよね。
その動きと同じ向きに、磁界がぐるりと回り込みます。
つまり、
- 電流が上へ進む → 磁界は右回り
- 電流が下へ進む → 磁界は左回り
という関係になります。
この「右回り／左回り」をつかんでおくと、
この先のローレンツ力の話もスムーズに理解できます。
手前・奥に流れる電流の記号（⦿と⊗）を覚えよう
電流が紙面の手前や奥に向かうときは、矢印の代わりに次の記号を使います。
$$
\begin{aligned}
\textcolor{#B22222}{{⦿}} & : \text{手前に向かう電流} \\
\textcolor{#B22222}{{⊗}} & : \text{奥へ向かう電流}
\end{aligned}
$$
弓矢を真正面や背面から見たときの姿をイメージすると分かりやすいです。
この表記を理解しておくと、立体的な電流の向きでも磁界の回転方向を正しく判断できます。
これ、説明もなくイキナリ使われること多いんですよね。
ここで把握しておけば、医用工学でも役立ちますよ。
一様磁場の性質と向き
磁場の向きと強さがそろっている状態を一様磁場といいます。
この一様磁場の中に電流が流れると、電流自身が生み出す磁場と重なり、場所によって磁場の強さに差が生じます。
まずは、そのしくみを図といっしょに確認しましょう。
磁場は N 極から S 極へ向かって生じる
次の図を見てください。
縦向きの矢印は、一様磁場 B を表しています。
磁場の向きは N 極から S 極へ向かって上向き です。
すべての矢印が同じ向き・同じ長さで描かれていることから、
この空間が一様磁場であることが分かります。
図の中心に描かれた「⊗」は、電流が奥へ向かって進んでいることを示す記号です。
奥向きの電流は、右ねじの法則により周囲に右回り（時計回り）の磁界をつくります。
図の円は、この電流がつくる磁界の回り方を示しています。
ここで注目したいのが、場所によって一様磁場と電流の磁界の向きがどのように重なるか、という点です。
- ア地点では、電流がつくる磁界の向きが上向きの一様磁場と同じ向きになります。
→ 強め合う - イ地点では、電流がつくる磁界の向きが一様磁場と反対向きになります。
→ 弱め合う
このように、一様磁場の中では、外部の磁場と電流がつくる磁場が重なり、
場所によって磁場の強さに差が生じるのです。
よって磁場の強さがわずかに変化します。
一様磁場とは？ 強め合う・弱め合うのしくみ
磁場には、同じ向きで重なると強め合い、
逆向きで重なると弱め合う性質があります。
今回の図では、
- ア地点：磁場が強い
- イ地点：磁場が弱い
という分布が生まれます。
磁場の強弱に差があると、その差に応じて力がはたらきます。
図ではその力が F として描かれており、向きは「⊗ → イ」の方向です。
この力が、次のセクションで扱う ローレンツ力 です。
荷電粒子に働くローレンツ力
一様磁場の中で荷電粒子が動くと、
進行方向にまっすぐ進むだけではなく、
横向きに力を受けるようになります。
この力は、磁場と速度の両方がそろったときにだけ生まれる特別な力で、
ローレンツ力と呼ばれています。
ここでは、その大きさと向きがどのように決まるのかを整理していきましょう。
ローレンツ力 $\pmb{F＝qvB}$ の意味
ローレンツ力とは、
電荷 q をもつ粒子が速度 v で磁場 B の中を動くときに働く力
のことです。
その大きさは次の式で表されます。
$$\color{#B22222}{\pmb{F＝qvB}}$$
式に含まれる要素は非常にシンプルで、
- 電荷量 q が大きいほど力は大きくなる
- 速さ v が大きいほど力は大きくなる
- 磁場 B が強いほど力は大きくなる
という直感的に理解しやすい関係になっています。
特に大切なのは、電荷が正か負かによって力の向きが反転するという点です。
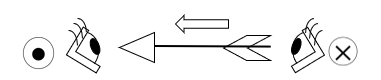
力の向きはどう決まる？ 左手の考え方で理解する
ローレンツ力の向きは、磁場と速度の向きに対して必ず直角になります。
この向きを立体的に判断するために使われるのが 左手を使った方法 です。
下の図を見てください。
左手の
- 人差し指が磁場の向き、
- 中指が電流（または正の電荷の速度）の向き
- 親指が力の向き
を表しています。
つまり、
磁場 × 電流（または速度）＝ 力の向き
という三つの関係を、一度に読み取れる便利な図解です。
正の電荷に注目すると、親指が示す方向にローレンツ力が働きます。
負の電荷（電子）であれば、その逆向きに力が働く点だけ注意が必要です。
速さは変えずに進む方向だけを曲げるという特性につながります。
ローレンツ力が円運動をつくる理由
磁場の中を荷電粒子が動くと、ローレンツ力が横向きに働きます。
この力は、粒子の進む向きに直角に作用するという特徴をもっています。
では、この“直角に働く力”が、どうして粒子を円運動へ導くのでしょうか。
速さが変わらず進行方向だけ変わる理由
ローレンツ力は、粒子の進む向きに対して必ず直角に働きます。
直角に力が加わると、粒子は“横に引っ張られる”ように方向だけが変わります。
ここで大切なのは、
速さそのものは変化しない という点です。
力が進行方向と同じ向きに働けば粒子は加速しますが、
ローレンツ力はいつも横方向なので、
粒子は加速も減速もしません。
“速さはそのまま、向きだけが変わる”という動き方になるのです。
向心力としてローレンツ力が働くしくみ
進行方向が少しずつ横へ曲がっていくと、粒子の軌道は自然と円の形に近づきます。
ちょうど、ボールをひもにつないで回すと外側へ飛び出そうとするけれど、
ひもが中心へ向かって引っ張ることで円運動になるイメージです。
ここで“ひも”の役目をしているのが、ローレンツ力です。
ローレンツ力は常に “中心向き” に向きを変えようとする働き方をするため、
荷電粒子は円軌道に沿って進むようになります。
このとき、ローレンツ力は向心力として働いている、というわけです。
式で確認しよう（ $\pmb{F_c＝\frac{mv^2}{r}}$ と $\pmb{F_r=qvB}$ の比較）
円運動をするとき、粒子には中心に向かう力が必要です。
その大きさは、次の式で表されます。
$$\pmb{F_c＝\frac{mv^2}{r}}$$
一方、磁場中を速さ $v$ で動く電荷 $q$ には、ローレンツ力が働き、その大きさは
$$\pmb{F_r=qvb}$$
と表されます。
“円運動が起きる”というのは、この二つの力がつり合っているということです。
$$\pmb{qvb=\frac{mv^2}{r}}$$
この関係式から、粒子の軌道半径 $r$ は
$$\pmb{r=\frac{mv}{qB}}$$
となり、質量や速さ、磁場の強さによって円の大きさが決まることが分かります。
サイクロトロンなどの実際の機器でも、この性質がそのまま利用されています。
円運動の角速度にも注目してみよう
円運動では、粒子がどれくらいの速さで“くるくる回るか”を表す量として角速度（ $\pmb{\omega}$ ） がよく使われます。
角速度は、円の半径 $r$ と速さ $v$ の関係から
$$\pmb{\omega=\frac{v}{r}}$$
と表されます。
ここに、先ほど求めた
$$\pmb{r=\frac{mv}{qB}}$$
を代入していくと、
$$\pmb{\omega=\frac{qB}{m}}$$
となります。
ここでのポイントは、角速度は粒子の速さ $v$ に依存しないということです。
- 質量 $m$ が大きい → ゆっくり回る
- 電荷 $q$ が大きい → 速く回る
- 磁場 $B$ が強い → 速く回る
といった特徴が、式を見るだけで読み取れます。
この性質は、後で学ぶ装置（サイクロトロン）でもそのまま活かされており、
国試でも頻繁に問われる重要ポイント です。
周期にも軽く触れておこう
円運動では、1回転にかかる時間のことを周期（ $\pmb{T}$ ）といいます。
角速度 $\omega$ が分かると、周期は次のように表せます。
$$\pmb{T=\frac{2\pi}{\omega}}$$
ここでは式の形だけ紹介しておきますが、この周期の式は
サイクロトロンの動き方や、後で学ぶ 国試頻出の計算 に深く関係しています。
詳しい導き方は、別の記事（F07）であらためて解説する予定です。
サイクロトロンへの応用
これまで見てきたように、荷電粒子は磁場の中を動くと円運動をします。
この性質をうまく利用すると、粒子を効率よく加速する装置を作ることができます。
その代表が サイクロトロン です。
ここでは、仕組みのイメージをシンプルにつかんでおきましょう。
サイクロトロンの仕組み
サイクロトロンは、磁場と電場を組み合わせて粒子を加速する装置です。
中央には2枚の金属電極が向かい合って置かれており、
この電極の形がアルファベットの D に似ていることから、
D 電極 （単にDとも言われる）と呼ばれています。
粒子はまず中央付近から出発し、
磁場によって円運動しながら、D 電極の中をぐるぐる回ります。
このとき、電極の間にかけられた電圧がタイミングよく切り替わることで、
粒子は D 電極を通過するたびに少しずつエネルギーを増やしながら回転 していきます。
回転しながら外側へ向かっていくのは、
粒子の速さが増えるにつれて円軌道の半径が大きくなるためです。
このようにして、粒子は装置の外周に近づくほど高いエネルギーをもつようになります。
サイクロトロンの動作には、
先ほど学んだ「ローレンツ力による円運動」や
「角速度が粒子の速さに依存しないこと」が深く関係しています。
これらの性質のおかげで、粒子が電極を通過するタイミングを一定に保つことができるのです。
サイクロトロンの詳しい計算や周期の扱いについては、別の記事であらためて学ぶことにしましょう。
実際の問題を見ていきましょう
第55回 2003年 問22
一様な磁束密度 $B$ を持つサイクロトロンの回転運動の角速度はどれか。ただし、加速される粒子の質量を $m$ 、電荷を $q$ とする。
- $\frac{m}{qB}$
- $\frac{B}{mq}$
- $\frac{mB}{q}$
- $\frac{qB}{m}$
- $\frac{mq}{B}$
解答を確認する。
正解は 4 です。
サイクロトロンの定番、式変形の問題です。
これは出題頻度も高いので、是非マスターしておきたいところです。
ポイントは問題文で定義されていない文字をどうやって消していくかです。
式変形のプロセスを示しておきます。
2～3回練習すれば、解けるようになると思います。
$$
\begin{aligned}
\text{向心力}&=\text{ローレンツ力}\\[6pt]
F_c&=F_r\\[6pt]
\frac{mv^2}{r}&=qvB\\[6pt]
\frac{v}{r}&=\frac{qvB}{mv}\\[6pt]
&=\frac{qB}{m}
\end{aligned}
$$
医療現場でのかかわり
ローレンツ力や磁場による円運動は、実際の医療現場でも利用されています。
代表的な装置がサイクロトロンです。
サイクロトロンでは、磁場中で荷電粒子を円運動させながら加速し、高速になった粒子を標的物質に衝突させます。
この反応によって、PET検査で使用される放射性同位元素（RI）が製造されています。
つまり、ここで学んだ
- ローレンツ力
- 円運動
- 向心力
- サイクロトロン
は、単なる試験対策ではなく、実際の核医学検査を支える技術にもつながっているのです。
まとめ
この記事では、ローレンツ力によって荷電粒子が円運動する仕組みについて見てきました。
最後にポイントを振り返ってみましょう。
- 電流のまわりにはアンペール右ねじの法則に従って磁場が発生する
- 一様磁場中では、荷電粒子にローレンツ力が働く
- ローレンツ力の大きさは $\pmb{F_r=qvB}$
- ローレンツ力は進行方向に直角に働くため、速さを変えずに向きだけを変える
- ローレンツ力は向心力として働き、荷電粒子を円運動させる
- 円運動の角速度は $\pmb{ω=\frac{qB}{m}}$
- この性質はサイクロトロンで利用されている
・まずは F＝qvB と ω＝qB/m の関係をしっかり押さえておきましょう。
・ローレンツ力は「vBq（バーベキュー）」で楽しく覚えましょう！
次に読むならコレ！レントゲン博士のおすすめ内部リンク
次はこの辺りも参考になるかもよ。
この記事を書いた人
たなまる
詳しいプロフィールはこちら
診療放射線技師・医療系専門学校専任教員。
都内大学病院で9年間勤務後、
2015年より医療系専門学校の専任教員として
放射線物理学・核医学・医用工学・放射線計測学・放射化学
などの講義を担当しています。
国家試験対策用ワークブックの制作や学習支援サイト「勉強嫌いの放物」の運営を行っています。
保有資格：
・診療放射線技師
・第1種放射線取扱主任者
・作業環境測定士
・衛生工学衛生管理者
ほか、放射線関連国家資格を保有
コメント