C05　X線管で生まれる制動放射線の仕組みを理解しよう！

「電子をぶつけるだけでX線が出る」――そう聞くと、ちょっと不思議に感じませんか。
しかも、そのX線には“いろんな波長”が混ざっていて、ひとつの線じゃなく連続した光の分布になるんです。

実はこれ、電子がターゲットにぶつかったときに減速してしまうことが原因。
そのとき失ったエネルギーが、そっくりそのままX線として放たれるんです。

この記事では、そんな制動放射線の仕組みをやさしくたどりながら、
クラマースの式やクーレンカンプの式が“何を教えてくれるのか”も一緒に見ていきます。

X線管の中で起きていることがわかると、装置の出力や撮影条件の意味も、きっと違って見えてくるはずです。

X線はどうやって生まれるの？

X線管の中では、目に見えない世界で壮大なエネルギーの変換が起きています。
電気の力で電子を加速し、それがターゲットに衝突することで光が生まれる――。
ここでは、その一連の流れを順を追って見ていきましょう。

電子を加速してターゲットへ

X線が生まれる最初の舞台は、陰極（フィラメント）です。
ここに電流を流すと熱せられ、表面から電子が飛び出します。
このように、熱によって放出される電子を熱電子と呼びます。

放たれた熱電子は、真空中を漂う間もなく、強力な電場に引き寄せられます。
その電場を生み出しているのが、反対側の陽極（ターゲット）です。
陰極と陽極のあいだには高い電圧（管電圧）がかかっており、
電子はその電位差によって一気に加速されていきます。

たとえば管電圧が100 kVなら、1個の電子が得るエネルギーは100 keVになります。
この関係については、A2の記事「放射線物理に必要な物理単位まとめ｜速度・圧力・電気など12個を簡単整理」で扱いましたね。
加速された熱電子は光速の半分ほどの速さにまで達し、そのままターゲット金属へ突っ込んでいきます。

つまり、陰極で生まれた熱電子が、陽極へ向かって走る――
この“走るエネルギー”こそが、のちにX線のもとになる運動エネルギーなのです。

減速すると光る？ 制動放射の基本原理

陽極ターゲットに突っ込んできた（入射した）電子たちは、そこでいきなりブレーキをかけられます。
ターゲット内部には原子核がぎっしり詰まっており、その正の電荷が電子を強く引き寄せるからです。
電子はその引力に引かれながら進路を曲げられ、まるで急カーブを切る車のように減速します。

このとき、電子は“進む力”を少し失い、そのエネルギーが電磁波（＝X線）に変わります。
これが制動放射（Bremsstrahlung）という現象で、このときに放出されたX線は制動放射線と呼ばれます。
ドイツ語で「ブレーキ放射」という意味の通り、電子がブレーキを踏むたびに光が生まれる――そんな現象です。

ただし、「止まったとき」ではなく、「曲げられた瞬間」に放射されることがポイントです。
電子がどれくらい強く引き寄せられたか、つまりどれだけ急に方向を変えたかによって、
放たれるX線のエネルギー（＝波長の短さ）が変わります。

たとえば、ほとんど減速せずに通り過ぎた電子は、低エネルギーのX線しか出しません。
一方で、原子核のすぐそばを通って大きく減速した電子は、
持っていた運動エネルギーをほぼすべて放出してしまい、高エネルギーのX線を放ちます。

このように、電子ごとに減速の度合いが違うため、
X線（制動放射線）のエネルギーも一様ではなく、様々はエネルギーが連続的に混在する連続スペクトルとして現れるのです。
だから制動放射線は、波長の幅を持った“なだらかな山形”のグラフを描きます。

制動放射の性質をつかもう

制動放射線は“減速の度合い”によって生まれるエネルギーが変わるため、
一つひとつの電子が放つX線にばらつきがあります。
その結果として現れるのが、連続的に広がるスペクトル。
ここでは、その性質とエネルギーの上限を決める法則を見ていきましょう。

なぜ連続スペクトルになるのか

X線管で発生した制動放射線を波長ごとに分析すると、
山のように滑らかに連なるグラフが現れます。
これが連続スペクトルです。

原因はシンプルで、電子が減速する程度が毎回異なるからです。
原子核のすぐそばをかすめて一気に減速する電子もあれば、
遠くを通ってほとんどスピードを落とさない電子もあります。

たとえば、高速道路でいろんな車がそれぞれのタイミングでブレーキを踏むようなもの。
ブレーキの強さがバラバラなら、減速の仕方も、放たれる光（X線）のエネルギーもまちまちになります。
その結果、波長が短いX線から長いX線まで、連続的に分布するのです。

このグラフの形は、ターゲットの材質によって大きく変わることはありません。
銅でもタングステンでも、基本の形は同じです。
つまり制動放射の連続スペクトルは、「電子が減速するという現象そのもの」によって決まっているのです。

最短波長とデュアン・ハントの法則

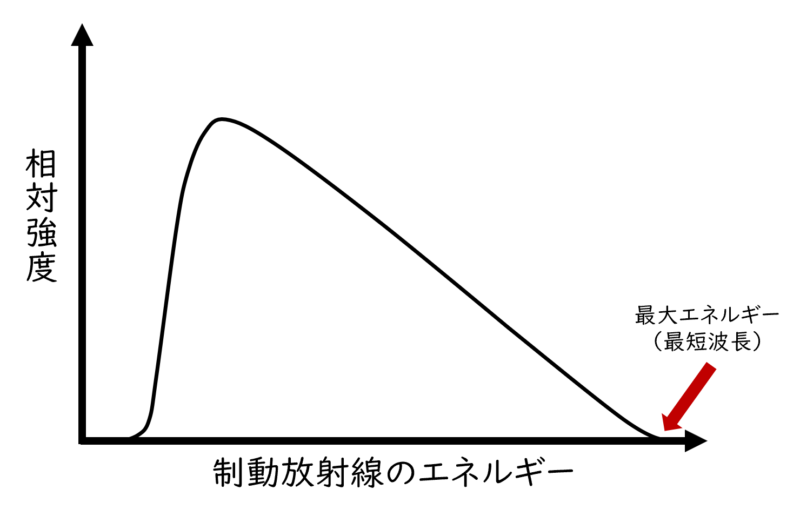
制動放射のスペクトルには、右端に“打ち止め”のような位置があります。
これより高いエネルギーのX線は出ません。
ここが制動放射線の最大エネルギーとなります。
また、エネルギーと波長の関係式は以下のようになっています。

$$ E=\frac{hc}{λ} $$

ここで、h：プランク定数、c：光速、E：制動放射線のエネルギー、λ：波長です。

つまり、制動放射線のエネルギーが最も高いとき、波長は最も短くなります。
これを最短波長と呼び、その位置を決めるのがデュアン・ハントの法則です。

法則の内容はとても単純で、
「電子の持っていた全エネルギー（＝加速電圧）を、まるごと1個のX線に変えたとき」
そのX線の波長が最短になる、というものです。

式で書くと次のようになります。

$$
\color{#B22222}{
\pmb{
\begin{aligned}
\lambda_{\min} &= \frac{hc}{eV} \\[6pt]
&= \frac{1.24}{V}
\end{aligned}
}
}
$$

ここで、
h：プランク定数、c：光速、eV：電子のエネルギー（加速電圧×電荷）、V：kV単位の管電圧です。
この式で求められるのはnm単位の最短波長です。

たとえば管電圧を2倍にすると、電子のエネルギーも2倍になります。
すると最短波長は半分になり、より高エネルギー側までX線が広がります。
つまり、管電圧が高いほど硬い（エネルギーの高い）X線が得られるわけです。

この最短波長は、後で扱う「クラマースの式」や「クーレンカンプの式」のグラフでも、
スペクトルの端を決める重要な基準になります。

※スペクトルの端：スペクトルの横軸が波長なら左端、エネルギーなら右端にあたります。
※上の図では横軸がエネルギーなので、右端となります。

制動放射の強度分布を理論で見る

前のセクションでは、「制動放射」がどうやって生まれるかを感覚的に見てきました。
ここではもう一歩踏み込んで、「その強さがどう変わるのか？」を理論的に考えてみましょう。

制動放射では、加速電圧が大きいほど高エネルギーのX線が出やすくなりますが、
その分、低エネルギーのX線もたくさん混ざっています。
この“分布の形”を説明するために生まれたのが、
クラマースの式やクーレンカンプの式といった理論です。

どちらも、
「電子がターゲットにぶつかって減速するとき、どんなエネルギーのX線をどれくらい出すのか」
を数学的に表すものです。

つまり、制動放射線のエネルギー分布（強度分布）を示しているのです。

ではまず、基礎となるクラマースの式から見ていきましょう。

クラマースの式でわかること

クラマース（Kramers）の式は、制動放射のX線強度を最もシンプルな形で説明する理論です。
シンプルとは、古典量子論でという意味です。
つまり、制動放射線のエネルギー分布を古典量子論的に説明した式をクラマースの式といいます。

電子が金属ターゲットの原子核の電場で減速されるとき、
どんなエネルギーのX線を出すのか――それを“理想的な条件”で近似したものなんですね。

式の形はおおよそ次のように表されます。あくまでおおよそです。

$$I(E)=K\cdot Z\cdot (E_0-E)$$

ここで、

• I(E)：エネルギーEのX線強度
• Z：ターゲット金属の原子番号
• E₀：電子が持っていた最大エネルギー（＝加速電圧に対応）
• K：定数（比例関係の係数）

つまり、電子が持つエネルギー E₀​ から実際に放射されるX線のエネルギー E を引いた分だけ、強度が変わるという考え方です。
このため、グラフにすると「高エネルギー側でゼロに近づく直線的なスペクトル」になります。

クラマースの式のすごいところは、
実際のスペクトルの“全体的な形”をかなりよく再現できる点です。
細かいピーク（特性X線）は含まれませんが、
制動放射の“山なりの分布”を理解するうえでの出発点になるんです。

クーレンカンプの式とのちがい

クラマースの式は「理想的な条件下での近似式」でした。
つまり、電子が金属ターゲットにぶつかって減速する際、
エネルギー損失がなめらかに起こると仮定しているわけです。

でも、実際のX線管の中ではそんなに単純ではありません。
電子は金属原子の電場の中で、
さまざまな距離や角度で減速されるため、
放射されるX線の強さには微妙なばらつきが生じます。

この“現実のずれ”を補正するように提案されたのが、クーレンカンプ（Coulomb–Kramers）実験式です。
クラマース式をベースにしつつ、電子の速度やクーロン力の影響を考慮して改良されたものなんです。
クラマースの式に「実際の測定結果」をもとに補正を加えたものです。
複雑になってくるので、紹介は割愛します。
つまり、国試で式の中身は問われないということ。

式の詳細は複雑ですが、ざっくり言えばこうです。

• クーレンカンプの式では、電子と原子核との相互作用の確率（断面積）を取り入れている
• その結果、低エネルギー側のX線強度がより実測値に近づく

グラフで比べると、クラマース式はやや単純な直線的な分布、
クーレンカンプ式は少し丸みを帯びて、低エネルギー側が高めに補正されたカーブになります。

つまり――
クラマース式は“理想のモデル”、
クーレンカンプ式は“実際に近づけたモデル”という関係なんですね。

電子エネルギーとX線強度の関係

ここまでで、「クラマースの式」と「クーレンカンプの式」が
それぞれどんな特徴を持っているかを見てきましたね。
では、加速電圧──つまり電子のエネルギー──を変えると、
制動放射の強度はどう変わるのでしょうか？

これは直感的にも理解しやすくて、
電子のエネルギーが高いほど、ターゲット原子の電場に突っ込む勢いも強くなります。
そのぶん、より多くのエネルギーが放射（＝X線）として放たれるわけです。

式で表すと、クラマース式にも出てきたように
エネルギーの上限 E₀​（＝加速電圧）によってスペクトルの右端が決まります。
電圧を上げれば、その端（最短波長の位置）は右側にずれていき、
全体の強度も大きくなるという関係です。

クーレンカンプの式で見ると、この関係はさらにリアルで、
低エネルギー成分の強度増加も一緒に再現されます。
つまり、電圧を上げると「山全体が持ち上がる」ような変化を示すんですね。

---

まとめるとこうです。

• 電子のエネルギー（加速電圧）を上げると、X線強度が全体的に増える
• 最短波長は短くなる（＝より高エネルギーのX線が出る）
• 低エネルギー側も、クーレンカンプの式で見るとより現実に近いカーブになる

---

実際の過去問を見てみよう。

2008年に実施された第60回国家試験からのご紹介。
ちょっと古いですが、現在でも出題される可能性が十分にある内容です。

答えを確認する。

正解は　4　です。

できましたか？
デュエンハントの法則を使えば何のことはない計算問題です。
注意しなければならないのは、波長と管電圧の単位を意識することです。

計算過程はこのようになります。

$$
\boldsymbol{
\begin{aligned}
V&=\frac{1.24}{λ_{\min}}\\[6pt]
&=\frac{1.24}{2\times10^{-2}}\\[6pt]
&=62[kV]
\end{aligned}
}
$$

医療現場でのかかわり

私たちが病院で使っているX線のほとんどは、
この制動放射によって生まれています。

撮影用のX線管の中では、電子がターゲット金属にぶつかって減速し、
そのときに放たれたエネルギーがX線となって飛び出しているんです。

つまり、「制動放射がわからないと、X線撮影の原理がわからない」というくらい、
この現象は医療現場の根本に関わっています。

どんな検査でも、その背景にはこの小さな減速の瞬間がある――
そう思うと、X線管の中も少し身近に感じられますね。

まとめ

制動放射は、熱電子がターゲットにぶつかって減速するときに放たれるX線のこと。
そのスペクトルは“連続的”で、最短波長はデュエンハントの法則から管電圧のみで決まります。
そのエネルギー分布は理論的にクラマースの式で近似され、より実測に近づけた補正版がクーレンカンプの式です。

医療現場で使われるX線の大部分は、この制動放射によるもの。
つまり、この現象を理解することが、X線撮影の原理を理解することにつながります。

お願い

本サイトに掲載されている図やイラストの著作権は管理人にあります。
無断掲載や転載はお断りさせていただきます。

また、リンクフリーではありますが、画像などへの直リンクはお控えください。

次に読むならコレ！電爺的おすすめ内部リンク

• C1：X線の定義と種類
• B1：放射線とは何か？基本の定義と大まかな分け方

次に読むならコレ！たまのすけおすすめ外部リンク

・公益社団法人日本天文学会天文学辞典