
特性X線とかオージェ電子とか分かってきたけど、
計算になると止まっちゃいます……。

そんなん、ゴロで覚えたらええねん!
Kαはケアル※20、Kβはニコ(25)っとMAXと小さな兄さん(23)!
どや!完璧やろ!?


それ、エネルギー変わったら使えんじゃないかのぅ?
ひとつ、白魔法はいっとるし。

FFネタは嬉しいところだけどね。
語呂は入口にして、今日は“結合エネルギーの差”ってトコを押さえていこう。
※「ケアル」は『ファイナルファンタジー』シリーズ(発売元:スクウェア・エニックス)に登場する魔法名です。
特性X線やオージェ電子のことは覚えたのに、いざそのエネルギーを計算しようとすると手が止まる——そんな質問、よく受けます。
本記事では、エネルギーが「結合エネルギーの差」で決まる理由を押さえ、式に頼らず自分で導ける状態を目指します。
まず前提(どの殻からどの殻へ落ちるか)を言葉で整理し、次に数値を当てはめて、Kα・Kβ・Lα、そしてオージェ電子の順に短い例題で確認します。
このやり方は国家試験での計算問題でも使えますし、医療現場でのピーク識別や装置の理解にも役立ちます。
さっそく解答例
「初学 放射線物理学 ワークブック」検索番号 C04 の穴埋め解答例と解説です。
先に自分で穴を埋めてみてからの答え合わせでも良いですし、解答例を写してから覚えていっても良いです。ご自分に合ったスタイルで取り組んでください。
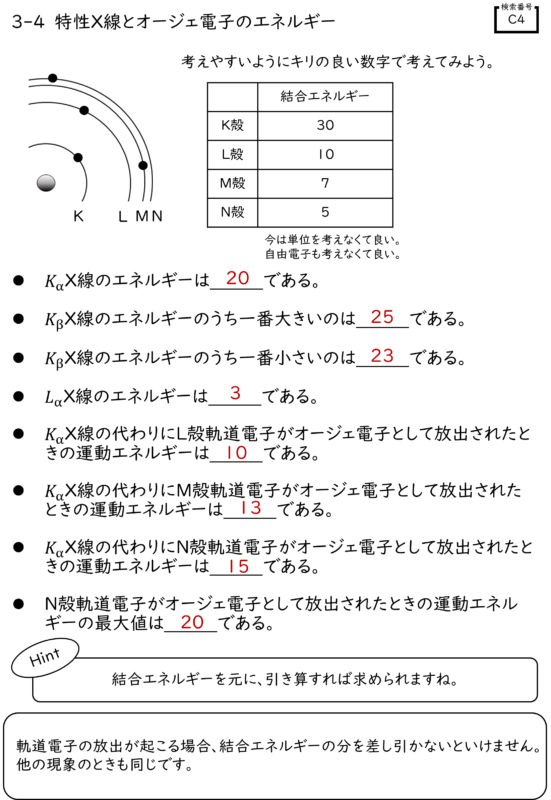
何が起きている?
原子の内側の殻に空位ができ、外側の殻から来た電子が遷移してそれを埋めます。
そのときのエネルギーが、特性X線として出るか、別の電子を電離してオージェ電子になるかの二択です。
この章ではまず、このしくみの全体図を押さえます。ポイントは「結合エネルギーの差」です。
内殻に空位ができるまで
- どうやって空位ができる?
X線や電子が当たって、内側の殻(K・Lなど)の電子が電離すると、その殻に空位ができます。 - なぜ内殻が大事?
内殻ほど結合エネルギーが大きく、外殻との差も大きいので、あとで出てくるエネルギーも大きくなります。 - 起こり方の例
- 光電効果:X線を吸収 → 内殻電子が電離 → 空位ができる。
- 衝突電離:電子線が当たる → 内殻電子が電離 → 空位ができる。
- ここでのゴール
「どの殻に空位ができたか(KかLか)」をしっかり認識できるようになりましょう。
空位の埋まり方は2通り:特性X線かオージェ電子か
- 遷移:外側の殻の電子が、空位のある内側の殻へ遷移して埋めます。
- エネルギーの行き先(2択)
1) 特性X線(光を出すほう)… 遷移のエネルギーがX線として出る。
2) オージェ電子(光を出さないほう)… そのエネルギーで別の電子が電離し、オージェ電子として飛び出す。 - ちょい知識
一般に軽い元素はオージェが起きやすく、重い元素は特性X線が目立ちやすい傾向があります。
この辺りはC2・C3で詳しく解説しています。そちらもご覧ください。
結合エネルギーと「差」のルール
原子の“どの殻からどの殻へ遷移したか”で、放出されるエネルギーが決まります。
ここで使うのは結合エネルギーの差だけです。
※結合エネルギーの差で計算しても、エネルギー準位の差で計算しても結果は同じになります。
結合エネルギー?エネルギー準位?ってなってしまった方はA21でおさらいしましょう。
結合エネルギーの定義と符号
- 定義:その殻の電子を原子から電離させるのに必要なエネルギー(eV, keV)。
- 大小関係:結合エネルギーは内側ほど大きい(例:K > L > M > N)。
- 符号の扱い:本記事では正の数として扱います(“必要量の大きさ”という意味)。
- 計算のコツ:以後、式はすべて「大きい − 小さい」の順で書きます。
特性X線:E =(空位がある殻)−(遷移元の殻)
- 考え方:外側の殻にいた電子が内側へ遷移して空位を埋めるとき、
その結合エネルギーの差が特性X線のエネルギーになります。 - 式のかたち:
– E = E(空位の殻) − E(遷移元の殻)
例:Kα(L→K)なら E = E(K) − E(L)。 - 意味づけ:
「空位のある殻の深さに“はまり直す”ぶんだけエネルギーが出る」。
オージェ電子:Ek =(空位の殻 − 遷移元の殻)−(放出される殻)
- 考え方:遷移で生まれたエネルギーが、別の殻の電子1個を電離させるのに使われ、
余りがその電子の運動エネルギー(オージェ電子のEk)になります。 - 式のかたち:
– Ek = E(空位の殻) − E(遷移元の殻) − E(放出される殻)
例:KLL なら Ek = E(K) − E(L) − E(L)。 - 意味づけ:
「遷移で得たエネルギー」から「もう1人を外へ出すための“結合エネルギー”」を差し引いた残り。
どの“差”を引く?
- Kα:L→K(空位:K、遷移元:L)→ E = E(K) − E(L)
- Kβ:M→K または N→K(どちらから来たかで値が変わる)
- M→K:E = E(K) − E(M)(Kβ “最小”)
- N→K:E = E(K) − E(N)(Kβ “最大”)
- Lα:M→L → E = E(L) − E(M)
チェックリスト(毎回これで確認できます)
- 空位の殻はどこ?(まずここを口で言う)
- 遷移元はどこ?(→ 特性X線の差が決まる)
- 誰が電離される?(→ オージェならさらにもう一つ引く)
- 式は大きい − 小さい(− 小さい)の順になっているか?
- 単位(eV/keV)を最後にそろえたか?
結合エネルギーで計算しても、エネルギー準位で計算しても同じになる
結合エネルギーの表で計算しても、エネルギー準位で計算しても、答えは同じになります。
理由はシンプルで、準位エネルギーが結合エネルギーと符号が逆なだけだからです。
- 用語の対応
- 結合エネルギー EB(殻):その殻の電子を原子から電離させるのに必要な量(正の数)
- 準位エネルギー Elevel(殻):真空を0としたときのその殻の“深さ”(負の数)
- 関係:Elevel(殻) = − EB(殻)
- 特性X線(Kαの例)
- 結合エネルギーで:E = EB(K) − EB(L) = 30 − 10 = 20
- 準位エネルギーで:E = |Elevel(L) − Elevel(K)| = |(−10) − (−30)| = 20
- オージェ電子(KLLの例)
- 結合エネルギーで:Ek = EB(K) − EB(L) − EB(L) = 30 − 10 − 10 = 10
- 準位エネルギーで:Ek = |Elevel(L) − Elevel(K)| − EB(L) = |(−10) − (−30)| − 10 = 10
- 使い分けのコツ
- 表が結合エネルギーで与えられていれば、そのまま差を引くのが早いです。
- 図が準位の深さなら、上の準位 − 下の準位の差の絶対値をとれば同じ答えになります。
基本例題(表:K=30, L=10, M=7, N=5)
ここでは「空位の殻」「遷移元」「(オージェなら)電離される殻」を言葉で決めてから、結合エネルギーの差をそのまま計算します。丸暗記は不要です。
Kα = 30 − 10 = 20
- 状況:K殻に空位。外側のL殻の電子が遷移して埋める。
- 式:E = E(K) − E(L) = 30 − 10 = 20
- メモ:Kαは「L→K」。空位の殻 − 遷移元の順。
Kβ:最大 25(N→K)/最小 23(M→K)〔最大・最小の理由〕
- 状況:K殻に空位。遷移元が M か N かで値が変わる。
- 式(最小):E = E(K) − E(M) = 30 − 7 = 23
- 式(最大):E = E(K) − E(N) = 30 − 5 = 25
- なぜ差が出る?:外側ほど結合エネルギーが小さい(M=7、N=5)。
したがって E(K) − E(より小さい数) のほうが差が大きくなり、N→Kが最大になります。
Lα = 10 − 7 = 3
- 状況:L殻に空位。M殻から遷移。
- 式:E = E(L) − E(M) = 10 − 7 = 3
- メモ:Lαは「M→L」。K系列と同じ考え方でOK。
まとめ表(特性X線)
| ライン | 遷移 | 計算式 | 結果 |
|---|---|---|---|
| Kα | L→K | 30 − 10 | 20 |
| Kβ(最小) | M→K | 30 − 7 | 23 |
| Kβ(最大) | N→K | 30 − 5 | 25 |
| Lα | M→L | 10 − 7 | 3 |
よくある取り違え
- L − Kのように小さい − 大きいと書かない。必ず空位の殻 − 遷移元。
- 記号だけ追って迷ったら、「Kに空位。どこから遷移?」と口で言ってから式にする。
オージェ電子のエネルギー(K空位)
「空位を埋める遷移で生じたエネルギー」を、別の電子の電離に使い、余りがその電子の運動エネルギー(オージェ電子 Eₖ)になります。
計算はかんたんで、「空位の殻 − 遷移元の殻 −(電離される殻)」の順に差をとるだけです。
仕組みを一歩ずつ(読み方のルール)
- 記号 KLM の読み方
1文字目 K:空位のある殻
2文字目 L:そこへ遷移してくる殻
3文字目 M:電離されて外へ出る殻(=オージェ電子がいた殻) - 基本式(結合エネルギーで表す):
Eₖ = E(空位の殻) − E(遷移元の殻) − E(電離される殻)
具体例(表:K=30, L=10, M=7, N=5)
- KLL: Ek = 30 − 10 − 10 = 10
(Kの空位をLからの遷移で埋め、そのエネルギーでLから電子が電離) - KLM:Ek = 30 − 10 − 7 = 13
- KLN:Ek = 30 − 10 − 5 = 15
- KNN(最大):Ek = 30 − 5 − 5 = 20
なぜ KNN が最大になる?
最後に引く「電離される殻」の結合エネルギーが小さいほど、引き算の余りが大きくなるからです。
N殻は L・M より小さい(5 < 7 < 10)ため、KNN が最大になります。
成立条件と注意
- Ek が 0 以上であること(負になれば、その組み合わせではオージェ放出は起きません)。
- 記号の順番に意味あり:1文字目=空位/2文字目=遷移元/3文字目=電離される殻。
- 途中で単位(eV / keV)を崩さないこと。
まとめ表(オージェ:K空位)
| 系列 | 意味 (空位/遷移元/電離) | 計算式 | 結果 |
|---|---|---|---|
| KLL | K / L / L | 30 − 10 − 10 | 10 |
| KLM | K / L / M | 30 − 10 − 7 | 13 |
| KLN | K / L / N | 30 − 10 − 5 | 15 |
| KNN | K / N / N | 30 − 5 − 5 | 20 |
よくあるミス
Kβの最大/最小の理屈をオージェにも混ぜる。→ オージェは最後に引く殻が小さいほど大。
順番を取り違える(例:L − K − L など)。→ かならず 空位 − 遷移元 − 電離殻。
記号の3文字目(電離される殻)を遷移元と勘違い。→ 3文字目は「外へ出る人」。

そうそう。やりがちじゃのぅ。
つまずきポイントとチェック
「差で考える」と言っても、計算の順番や記号の読み違いで止まりやすいところがあります。
ここではよくある誤り → 直し方 → 1行チェックの順で整理していきましょう。
引く順番の取り違え(L − Kにしない)
- 誤り:Kα を E = E(L) − E(K) としてしまう。
- 正解:空位の殻 − 遷移元の殻。Kα(L→K)なら E = E(K) − E(L)。
- 1行チェック:「空位はどこ?(K)→ どこから遷移?(L)→ K − Lの順で書く」
遷移する電子と、電離で出る電子の混同
- 誤り:KLM を「M→K の遷移」と読んでしまう。
- 正解:1文字目=空位/2文字目=遷移元/3文字目=電離される殻。
KLM は「空位:K、遷移元:L、電離:M」。 - 1行チェック:「空位→遷移→電離の順で3文字を読む」
単位と桁(eV / keV)
- 誤り:表は keV なのに、途中計算で eV に混在。
- 対処:開始時に単位を決めて最後まで固定。途中で変換したら、最後にもう一度単位を確認。
- 1行チェック:「最初に“keVで統一”とメモ」
ライン記号の読み分け(Kα / Kβ / Lα…)
- 誤り:Kβ を1種類だと思う。
- 正解:Kβ は遷移元の殻が複数あり(M→K と N→K)、最大/最小が生じます。
- 1行チェック:「Kβ=どこからKに遷移?(MかNか)」
オージェの“最大・最小”の考え方
- 誤り:KNN が最大になる理由を、特性X線のKβと同じノリで説明してしまう。
- 正解:オージェは Ek =(空位 − 遷移元)−(電離される殻)。
→ 最後に引く殻の結合エネルギーが小さいほど Ek は大きい。
N がいちばん小さいから KNN が最大。 - 1行チェック:「“最後に引く数が小さいほど大”」
チェックリスト
- 空位の殻はどこ?(K/L… を口で言う)
- 遷移元はどこ?(→ 特性X線の差が決まる)
- 電離される殻は?(→ オージェならもう一つ引く)
- 式の順番:空位 − 遷移元(− 電離殻) になっている
- 単位:eV/keV を最後にそろえる
ミニ演習
- 問1:Kβ(M→K)を表で求める(K=30, M=7)。
解答:E = 30 − 7 = 23 keV - 問2:KLM のオージェエネルギー(K=30, L=10, M=7)。
解答:Eₖ = 30 − 10 − 7 = 13 keV
ここまで押さえられたら、計算はもう“作業”になります。次は実際の過去問を見ていきましょう。
実際の過去問を見てみよう。

1994年に実施された第46回国家試験からのご紹介。
ちょっと古い問題ですが、大切な計算問題です。
答えを確認する。
正解は 2 です。
では、考え方を見ていきましょう。
計算問題は、まずは問われているものを確認します。
今回の場合は「光電子の運動エネルギーT」と「KαXのエネルギーEα」この2つです。
状況を図で示して、TとEαがどこに該当するかも見てみましょう。
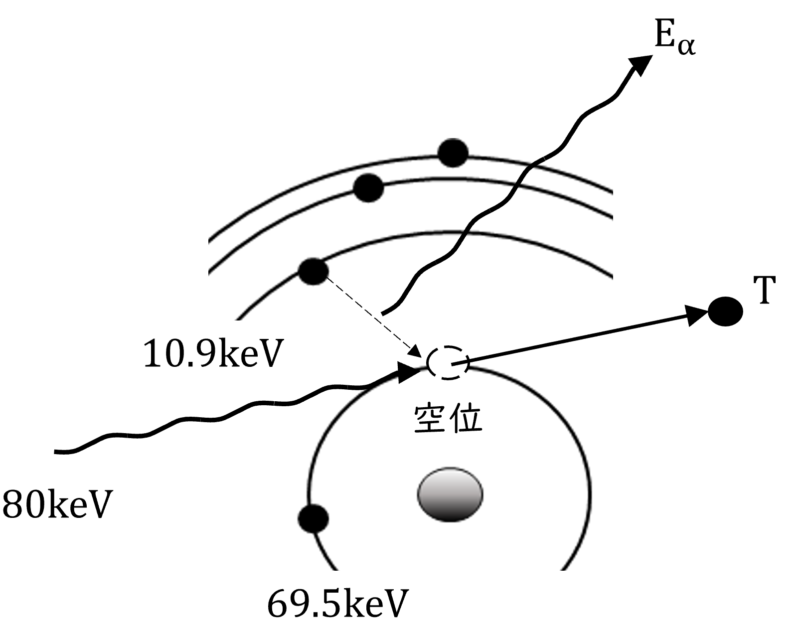
Kα線のエネルギー(Eα)が問われていることから、光電効果はK殻軌道電子で起きたことになります。
では現象の流れ的に光電子の運動エネルギーTから求めていきましょう。
80keVの入射光子が、結合エネルギー69.5keVのK殻軌道電子を電離します。
電離するには結合エネルギーを切断し、束縛から解放しなくてはいけません。
したがって、Tを求めるには
T= 80 – 69.5 = 10.5 keV
となります。
続いてEαを求めていきます。
Eαは結合エネルギーの差で求めることができます。
結合エネルギーの大きい方(69.5keV)から小さい方(10.9keV)を差し引けばOKです。
したがって、Eαを求めるには
Eα = 69.5 – 10.9 = 58.6 keV
となります。
医療現場でのかかわり
特性X線のエネルギーまで意識して撮影している技師は少ないと思いますが、マンモグラフィに携わっている場合は、そうも言ってはいられません。
エネルギーへの意識に関わらず、X線管球からは特性X線が出てきていますから、ご紹介しておきましょう。
X線管ターゲットの特性X線ピークを読む
一般撮影やCTで使うタングステン(W)ターゲットでは、スペクトル上にK系列の鋭いピークが立ちます。
本記事の「結合エネルギーの差」で考えると、Kα(L→K)やKβ(M/N→K)の位置関係を言葉で説明でき、線質管理やトラブルシュートに役立ちます。
- ここまで知っているとgood!
- 付加フィルタを変えると連続X線(制動放射線)の土台は削れても、特性X線のピーク位置は変わらない(強度は変わり得る)。※ここはC8、C9で解説しています。
- ターゲット材が変わればピークそのものの位置が移る(例:マンモではMo/Rhの低エネルギー側の特性X線を活用)。
要は、ピークは「殻どうしの差」の痕跡です。差の見方を持っていると、装置の設定や結果の変化を筋道立てて説明できます。
- C8:
- C9:
まとめ
本記事では、内殻に空位ができ、外側の電子が遷移してそれを埋める—この一連の出来事を軸に、エネルギーの行き先を整理しました。
特性X線は「空位のあった殻」と「遷移元の殻」の結合エネルギーの差で決まり、オージェ電子はその差からさらに「電離される殻」の結合エネルギーを差し引いた“残り”が運動エネルギーになります。
結合エネルギーの表で計算しても、準位の深さ(符号が逆)で計算しても結果は同じです。
計算の前には、空位→遷移→電離の順に状況を言葉で描き、式は「大きい数から小さい数を引く(必要ならもう一つ引く)」とだけ覚えておけば十分です。
単位は最後までそろえましょう。
医療現場では、タングステン管などで見える特性X線のピーク位置を、この“差”の考え方で説明できると線質の理解が速くなります。

結合エネルギーの差さえ言えれば、式はあとから付いてきます。
まずは電離→空位→遷移→特性X線orオージェ電子の順を確認してみましょう。
お願い
本サイトに掲載されている図やイラストの著作権は管理人にあります。
無断掲載や転載はお断りさせていただきます。
また、リンクフリーではありますが、画像などへの直リンクはお控えください。
次に読むならコレ!電爺的おすすめ内部リンク

ほれ、ここまで読んだんなら、次はこのあたりを見ておくとえぇぞい。
次に読むならコレ!たまのすけおすすめ外部リンク

ここまで読んできた皆さんなら、もう一歩踏み込んだ知識に触れてみたくなるはずです。そんな方におすすめの外部リンクを紹介しますね。
・X線の連続線と特性線(産総研:XAFS入門)
連続X線の土台+特性線ピークの説明が図で分かりやすいです。


コメント