単位ってたくさんあるけど、どの単位を覚えたらよいか、どこから手を付けたらよいか悩ましいですよね。
私もかつてそうでした。
単位は大事だから覚えろ！覚えろ！覚えろ！・・・と言われ続けてきました。
このページではよく出てくる単位をリストアップしてあります。
一気に覚えられなくても大丈夫。
使いながら覚えていきましょう。
単位を理解することで、単位の問題で得点できるようになるだけでなく、計算問題の立式もできるようになります。
放射線物理の学習に欠かせない「単位」の世界
放射線物理で登場する公式は、一見すると暗号のように感じられるかもしれません。
ですが、落ち着いて見てみると、その多くは「物理量と単位の組み合わせ」でできています。
たとえば、速度の単位は m/s。
これは「距離（m）を時間（s）で割ったもの」という意味です。
また、力の単位 N（ニュートン） は kg・m/s2 に分解でき、「質量 × 加速度」であることが見えてきます。
このように、単位は“意味のある組み合わせ”でできているのです。
それぞれの単位がどんな式から導かれ、どういう現象を表しているのかを理解すれば、公式をただ覚えるよりも、ずっと深く、そして長く記憶に残るようになります。
まずはこの記事で紹介する物理量と単位の一覧を掲載しておきます。
| 物理量 | 単位（記号） | 補足など |
|---|---|---|
| 速度 | m/s | 距離 ÷ 時間 |
| 加速度 | m/s² | 速度 ÷ 時間 |
| 力 | N（kg・m/s²） | 質量 × 加速度 |
| 仕事 | J（N・m） | 力 × 距離 |
| 仕事率 | W（J/s） | 仕事 ÷ 時間 |
| エネルギー | J, eV | エネルギーの大小で使い分け |
| 熱量 | J, cal | 熱の量を示す |
| 圧力 | Pa（N/m²） | 力 ÷ 面積 |
| 体積 | m³ | 長さ × 幅 × 高さ |
| 密度 | kg/m³, g/cm³ | 質量 ÷ 体積 |
| 電荷（電気量） | C | 電流 × 時間 |
| 電位差（電圧） | V | 電荷に働く力の大きさ |
| 静電容量 | F | 電荷 ÷ 電位差 |
| 電流 | A（C/s） | 電荷 ÷ 時間 |
| 電力 | W（J/s） | エネルギー ÷ 時間 |
| 抵抗 | Ω | 電位差 ÷ 電流 |
ここからは、放射線物理でよく登場する基本の単位16個を、ジャンル別に分けて1つずつ解説していきましょう。
単位が分かると、理解度が変わってきますよ。
まずは押さえたい！力学系の基本単位8つ
放射線物理の公式には、「力」や「エネルギー」といった力学的な概念がたくさん出てきます。
でも、それらはすべて「基本的な物理量」から積み上げてできているんです。
ここでは、そうした土台になる力学系の基本単位8つを、順に確認していきましょう。
速度の単位【m/s】
速度の単位は 【m/s】 です。
これは、
🟦 単位時間あたりに進んだ距離
を表しています。
たとえば「1秒間に1メートル進む」のであれば、それは 1 m/s という速度です。
これは「距離（m）を時間（s）で割ったもの」と考えるとわかりやすいですね。
逆に、10[km/h] という速度は「1時間で10km進む」ことを意味しており、
これをm/sに換算すると 10 ÷ 3.6 ≒ 2.78 [m/s] になります。
このように、速度の単位は「移動の速さ」を具体的に数値で表すものとして重要です。
加速度の単位【m/s²】
加速度の単位は 【m/s²】 です。
これは、
🟦 単位時間あたりに変化した速度の割合
という意味になります。
たとえば、1[m/s]の速さで動いていた物体が、2秒後に5[m/s]の速さで動いていたとしましょう。
このとき速度の変化量は 5 − 1 = 4[m/s]。
これをかかった時間 2秒で割ると、加速度は 4 ÷ 2 ≒ 2[m/s²] となります。
つまり加速度は、「速度の増え方を1秒ごとに見る」ようなイメージです。
速度は速さそのものを、加速度はその「変化の速さ」を表すという違いに注目です。
力の単位【N, kg・m/s²】
力の単位は 【N（ニュートン）】 です。
また、1Nは 【kg・m/s²】 に分解することができます。
その定義は、
🟦 物体に加速度を与える原因となる外からの影響
たとえば 2kg の物体を 3[m/s²] の加速度で動かすためには、
F = m × a = 2 × 3 = 6[N] の力が必要ということになります。
この「F = ma」という関係は、高校物理でよく登場する基本式ですね。
単位を分解してみると、
- 質量：kg
- 加速度：m/s²
→ よって力：kg・m/s²
つまり、「質量 × 加速度」という意味のある掛け算で、ニュートンという単位が成り立っているのです。
どうでしょう？
単位も分解すれば意味が見えてきませんか？
仕事の単位【J, N・m】
仕事の単位は 【J（ジュール）】 です。
また、N・m（ニュートンメートル） とも表されます。
定義としては、
🟦 物体に力を加えて動かしたときに生じるエネルギーのやりとり
です。
たとえば、10[N] の力で物体を 2[m] 動かした場合、仕事 W = F × d = 10 × 2 = 20[J] となります。
このように、「力 × 距離」という形で計算され、仕事をしたぶんだけエネルギーを消費したことになります。
仕事率の単位【W, J/s】
仕事率の単位は 【W（ワット）】 です。
また、J/s（ジュール毎秒） とも表されます。
定義は、
🟦 単位時間あたりに行った仕事の量
です。
たとえば、60[J] の仕事を 2秒で行ったとすると、仕事率 P = 60 ÷ 2 = 30[W] になります。
このように、「仕事 ÷ 時間」という形で計算され、「どれだけ短時間のうちにエネルギーを使ったか」を示す指標になります。
圧力の単位【Pa, N/m²】
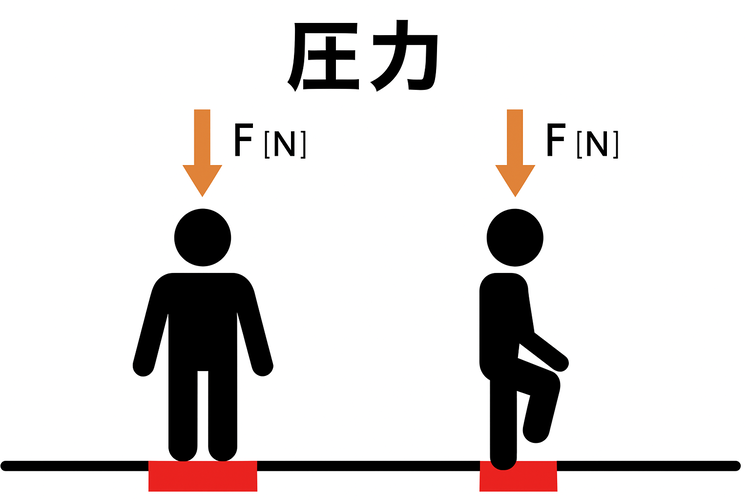
圧力の単位は 【Pa（パスカル）】 です。
また、N/m²（ニュートン毎平方メートル） とも表されます。
定義としては、
🟦 面積あたりに加わる力の大きさ
です。
たとえば、同じ50[N]の力でも、
1m² にかければ 50 ÷ 1 = 50[Pa]、0.01m² にかければ 50 ÷ 0.01 = 5000[Pa] と圧力は大きくなります。
つまり、「同じ力でも、面積が小さいほど圧力が大きくなる」という性質があります。
体積の単位【m³】
体積の単位は 【m³】（立方メートル）です。
定義はシンプルで、
🟦 物体が占める空間の大きさ
です。
体積は、縦 × 横 × 高さ で計算できます。
たとえば、各辺が 1[m] の立方体なら、1 × 1 × 1 = 1[m³] の体積をもつということになります。
放射線物理では「密度」とセットで出てくることが多いので、次とあわせて理解しましょう。
密度の単位【g/cm³, kg/m³】
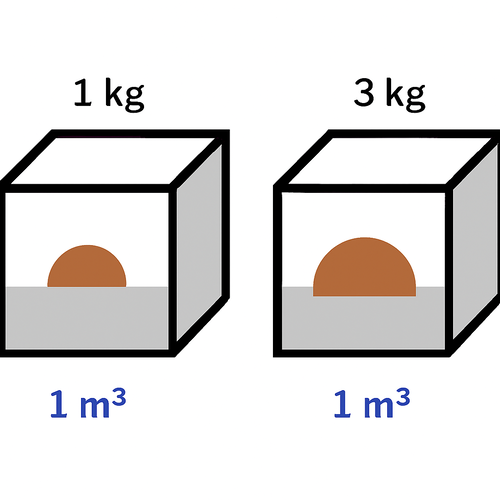
密度の単位は 【kg/m³】 または 【g/cm³】 です。
その定義は、
🟦 単位体積あたりの質量
です。
たとえば、1m³ に 500kg の物体が詰まっていれば、密度は 500 ÷ 1 = 500[kg/m³] ということになります。
つまり、「質量 ÷ 体積」という形で表され、同じ大きさでも中身が詰まっていれば密度が大きくなるという直感と一致します。
電気系の単位もしっかり確認しよう
放射線物理では、電気に関わる概念もたびたび登場します。
特にX線管や加速器、コンデンサに関連する場面では、電荷や電圧、電力などの単位を正しく理解しておくことが大切です。
ここでは、電気に関する6つの基本単位について、それぞれの意味と計算の関係を確認していきましょう。
電荷（電気量）の単位【C】
電荷（電気量）の単位は 【C（クーロン）】 です。
定義としては、
🟦 電流が一定時間流れたときに移動する電気の量
です。
たとえば、1アンペア（1A）の電流が1秒間流れたとき、電荷は 1 × 1 = 1[C]（クーロン） となります。
つまり、電荷 Q = 電流 I × 時間 t という関係が成り立ちます。
電位差（電圧）の単位【V】
電位差（電圧）の単位は 【V（ボルト）】 です。
定義は、
🟦 電荷を移動させるために必要なエネルギーの強さ
です。
たとえば、1[C] の電荷を 5[V] の電圧で加速したとき、得られるエネルギーは 1 × 5 = 5[J] になります。
このことから、J = C × V の関係があることがわかります。
静電容量の単位【F】
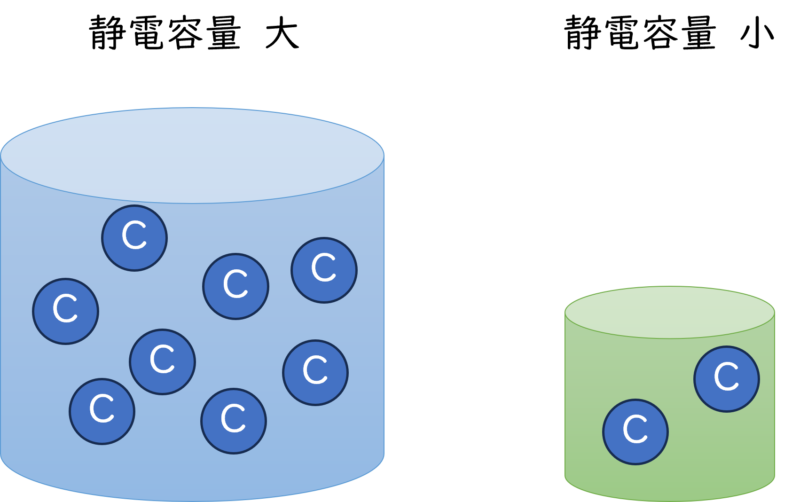
静電容量の単位は 【F（ファラド）】 です。
その定義は、
🟦 電位差あたりに蓄えられる電荷の量
です。
言い換えると、F = C ÷ V。
たとえば、1[V] の電圧で 3[C] の電荷を蓄えられるなら、容量は 3[F] です。
放射線機器では、コンデンサに蓄えられたエネルギーが一気に放出される場面もあり、容量の単位も重要です。
電流の単位【A, C/s】
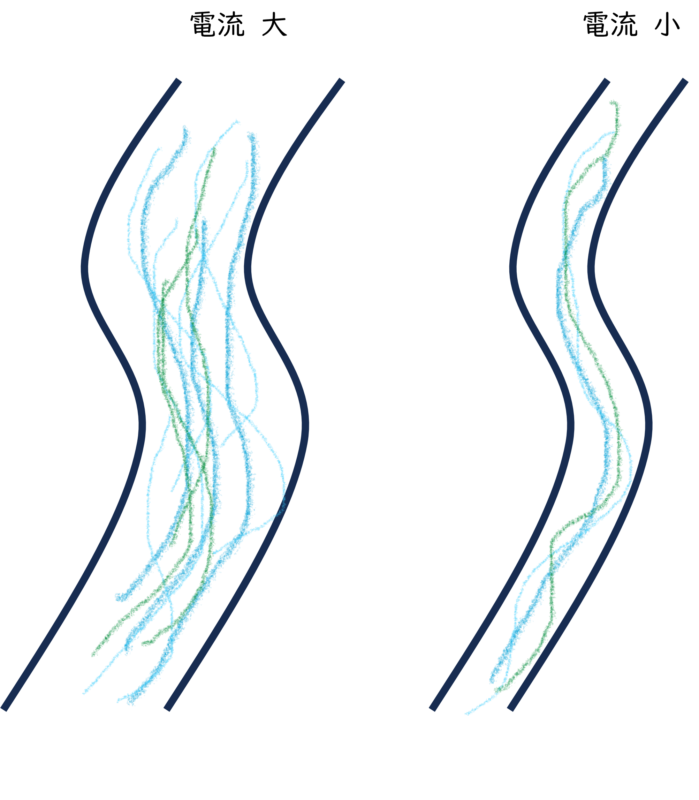
電流の単位は 【A（アンペア）】 または 【C/s（クーロン毎秒）】 です。
定義としては、
🟦 単位時間あたりに流れる電荷の量
です。
たとえば、2[C] の電荷が1秒間で流れた場合、電流は 2 ÷ 1 = 2[A] となります。
式で表すと、I = Q ÷ t。
電力の単位【W, J/s】
電力の単位は 【W（ワット）】 または 【J/s（ジュール毎秒）】 です。
定義は、
🟦 単位時間あたりに使われるエネルギーの量
です。
たとえば、10[J] のエネルギーを2秒で使った場合、電力は 10 ÷ 2 = 5[W]。
つまり、P = E ÷ t という形で表されます。
この「どれだけ短時間のうちにエネルギーを使ったか」が電力の意味です。
抵抗の単位【Ω】
抵抗の単位は 【Ω（オーム）】 です。
定義は、
🟦 電流の流れにくさ（電気の通しにくさ）
です。
オームの法則 V = I × R により、R = V ÷ I の形で求められます。
たとえば、5[V] の電圧で1[A] の電流が流れるとき、抵抗は 5 ÷ 1 = 5[Ω] です。
エネルギーと熱の単位も理解しよう
ここからは、放射線物理でとてもよく登場する エネルギー と 熱量 の単位を確認していきます。
どちらも物理では基本的な量ですが、単位の種類が複数あったり、似た記号が登場したりして混乱しやすい領域です。
ここで整理しておくと、後に出てくる電離・励起・光子エネルギーなどの話がスムーズにつながります。
エネルギーの単位【J, eV】
エネルギーの単位は【J（ジュール）】と【eV（エレクトロンボルト）】です。
定義は、
🟦 電荷を電圧で加速したときに得られるエネルギーの大きさ
です。
たとえば、電荷量が Q［C］の粒子に V［V］の電圧をかけるとき、
その粒子が得る運動エネルギー E は
$$
\color{#B22222}{
E=\left|Q\right| \, V \mathrm{[J]}
}$$
と表されます。
「電荷量 × 電圧」でエネルギーが決まる、という形になっていることを確認しておきましょう。
電子 1 個の電荷は、電気素量 e（約 1.6×10⁻¹⁹［C］）です。
この電子 1 個を V［V］だけ加速したときのエネルギーは
$$
E= V \mathrm{[eV]}
$$
となります。
これが「1 eV は電子 1 個を 1 V だけ加速したときのエネルギー」という定義につながります。
そして、電子1個が1[V]の電圧で加速したときに得られる運動エネルギーEは 1 [eV]と表される。
同じ考え方を一般の電荷量 Q に広げると、エネルギーを eV で表した式は
$$
E=\frac{\left|Q\right|}{e} \times V \mathrm{[eV]}
$$
となります。
放射線の世界では、X線やガンマ線の光子エネルギー、加速電子のエネルギーなどを表すときに、この【eV】（やその倍数の【keV】【MeV】）がよく使われます。
熱量の単位【J, cal】
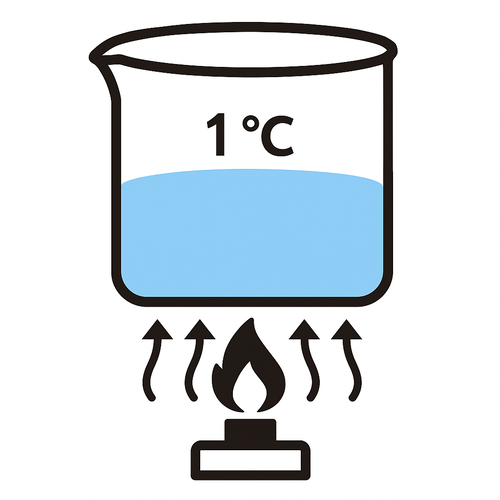
熱量の単位は【J】と【cal（カロリー）】です。
定義は、
🟦 水 1 g の温度を 1 ℃ 上げるのに必要なエネルギーの量
です。
カロリーはもともと熱を扱う分野で使われてきた単位で、現在は SI 単位である【J】に換算して扱います。
両者の関係は
1 cal ＝ 4.2 J
となります。
エネルギーも熱量も、本質的には同じ「エネルギー」の仲間です。
単位の意味と、この換算関係を押さえておくと、のちに出てくる線量や線量当量の学習がぐっと整理しやすくなります。
実際の問題を見ていきましょう
今回は第1種放射線取扱主任者試験からの1題です。
2016年に実施された第61回から。
第61回 2016年 問23
- 等価線量 $m^2 \cdot kg^{-1} \cdot s^{-1}$
- 線減弱係数 $m$
- 衝突断面積 $m^{-2}$
- 粒子フルエンス $m^{-2} \cdot s^{-1}$
- 質量エネルギー吸収係数 $m^2 \cdot kg^{-1}$
解答を確認する。
正解は 5 です。
- 等価線量の単位は [Sv] もしくは [J/kg] です。JをSI単位で置き換えると [m2/s2] となります。
- 線減弱係数の単位は [1/m] です。
- 衝突断面積の単位は [m2] です。
- 粒子フルエンスの単位は [1/m2] です。
- 正しいです。
医療現場ではこの知識がどう役立つの？
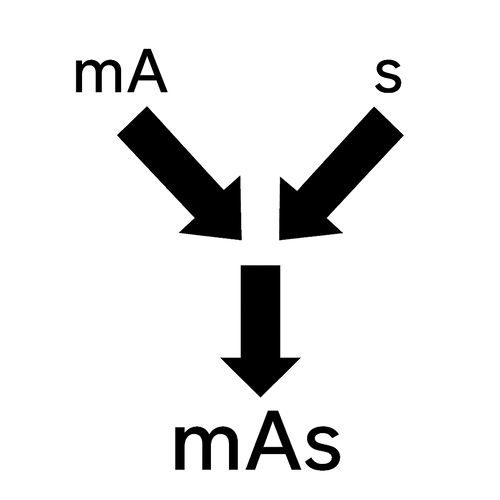
放射線検査では、単位の知識がそのまま検査条件の理解につながります。
その中でも mAs値 は、画像の明るさやノイズの量を左右する重要な指標です。
mA（電流）と s（時間）の組み合わせで決まる量であり、ここまで学んできた「単位の意味」を踏まえて考えると、その役割が見えてきます。
実際の胸部や四肢の撮影では、mAs値が大きいほどX線の総量が増え、画像が明るくなりノイズが減ります。
逆に mAs が小さすぎると、量子モトルが増えて読影しづらい画像になってしまいます。
つまり、mA と s の掛け算である mAs は、X線の“量”を決める指標として使われているのです。
単位の理解があると、
「なぜ時間を短くしたのに明るさが足りなくなったのか」
「動きの多い部位で時間を短くするなら、どれだけ電流を増やせば良いのか」
といった判断が自然につながるようになります。
mAs の意味を押さえておくことは、装置設定を感覚ではなく根拠を持って選べるようになる、医療現場における大切な基礎になっています。
量子モトルっていうのは線量が少ないことによって生じる統計的なノイズのことだよ。
量子モトルが大きいとノイズが多くて、ダメな画像ってことなんだ。
まとめ
この記事では、速度・圧力・電気量・エネルギーなど、放射線分野で欠かせない多くの単位を確認しました。
単位を理解しておくことは、個々の物理量をばらばらに覚えるのではなく、それぞれがどう関係しているのかをつかむ手がかり になります。
装置の設定値や画像の成り立ちを読み解くうえで、単位の意味を押さえておくことが大きな助けになります。
単位を知っておくと、いろんな物理量がどうつながっているのかが分かりやすくなるんだよ。
ひとつひとつの意味をゆっくり整理していこうね。
漫言放語（まんげんほうご）
先生…また”単位”って言葉が出てきました…
おれも高校のとき、”kg・m²/s³”とか出てきて泣いたわ
でもそれ、ちゃんと意味があるんだよ？理科界の美しさが詰まってる。
いや待てよ。牛助、高校行ってたんだね？
農業高校で育てられる側だけどね。
・・・
・・・
お願い
本サイトに掲載されている図やイラストの著作権は管理人にあります。
無断掲載や転載はお断りさせていただきます。
また、リンクフリーではありますが、画像などへの直リンクはお控えください。
次に読むならコレ！電爺的おすすめ内部リンク
ほれ、ここまで読んだんなら、次はこのあたりを見ておくとえぇぞい。
次に読むならコレ！たまのすけおすすめ外部リンク
ここまで読んできた皆さんなら、もう一歩踏み込んだ知識に触れてみたくなるはずです。そんな方におすすめの外部リンクを紹介しますね。
コメント