質量欠損や結合エネルギーの意味はなんとなくわかるけど、いざ計算問題になると「どこから手をつけていいのかわからない……」と手が止まってしまう。
あるあるですね。
私の友人にもいましたな。計算問題になるとアレルギー起こすやつ。笑
でも、ご安心を。
この記事では計算の流れを具体的に追っていきます。
重水素や4Heを題材に実際に手を動かすことで、「どうやって解けばいいか」がつかめるようになるはずです。
まずは重水素を例に解いてみましょう。
手取り足取り一緒に見ていきますから、じっくりやってみましょう。
その後ちょびっとヒントを与えつつ、4Heで考える練習。
最後は12Cの国試問題に挑戦する。
そんな3段構えです。
質量差を数値で出してエネルギーに換算する。
このステップを繰り返すことで、手順が自然に身につきます。
計算ができると「質量欠損=結合エネルギー」の理解もより実感を伴ったものになるでしょう。
質量欠損は覚えていますか?
落ち着いて取り組めば、中学生でもできる計算問題です。
やっかいなのは、桁数が異常に多いところ・・・

A15:原子核の質量が軽くなる?質量欠損とエネルギーでご紹介した「バラバラのときの質量の合計からくっついたときの質量を引く」ことを利用していきます。
これは質量欠損でしたね。
では重水素を例に見ていきましょう。
重水素を例に計算してみよう
まずは基本中の基本として、重水素(²H)を例に質量欠損と結合エネルギーを求めてみましょう。
一緒に式を追っていくので、落ち着いて進めてください。
重陽子(原子)の構成を確認
まずは重陽子の構成を確認しましょう。
ここで間違い・勘違いがあると正解にたどり着くことはありません。
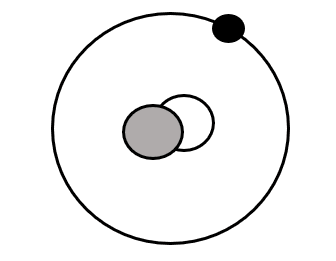
重陽子は正の電荷をもつ陽子1個、電荷をもたない中性子1個、負の電荷をもつ電子1個で構成されています。
※重陽子”原子”で考えています。重陽子”原子核”の場合は電子は含まれません。
必要な数値を確認
次に、計算に必要な数値を確認しておきましょう。
- 陽子の質量:1.007276 Da
- 中性子の質量:1.008665 Da
- 電子の質量:0.000548 Da
- 重水素(²H)の原子質量:2.014102 Da
桁数が多くて嫌になりますが、小数点の位置をキッチリ縦に揃えて間違わないように注意しましょう。
バラバラにした質量の合計を出す
重水素は陽子1個・中性子1個・電子1個から成り立ちます。
したがって、バラバラにしたときの合計質量は次のように計算します。
$$ 1.007276+1.008665+0.000548=2.016489 \,\mathrm{Da}$$
質量欠損⊿mを計算する
次に、バラバラにしたときの合計質量から実際の重水素の原子質量を引きます。
$$⊿m=2.016489-2.014102=0.002387 \,\mathrm{Da}$$
これで質量欠損が求まりました。
エネルギーEに換算する
質量欠損はエネルギーに変換することができます。
結合エネルギーでしたね。
1 Da = 931.5 MeV という具合に換算できるので、重水素の場合はこうなります。
$$
\begin{aligned}
E&=0.002387 \times \color{#B22222}{931.5}\\[6pt]
&=\text{約}2.223\,\mathrm{MeV}
\end{aligned}
$$
結果と意味を整理してみよう
重水素の質量欠損は 0.002387 Da、これに相当する結合エネルギーは 約2.2 MeV でしたね。
つまり、重水素の原子核をバラバラにするには2.2 MeVものエネルギーが必要ということになります。
逆に言えば、核ができるときにこのエネルギーが放出されて安定している、ということでもあります。
4Heで練習してみよう
それでは、4Heでも先ほどと同じようにやってみよう。
粒子の数と質量を確認
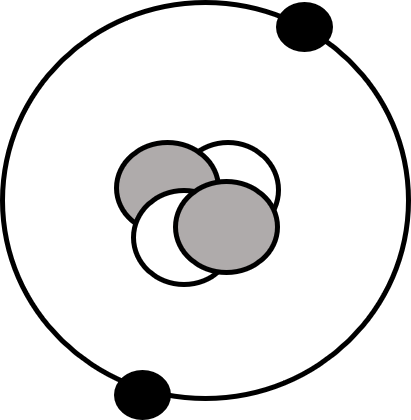
Hint:まずは「バラバラの合計質量」を出してから、実際の原子質量を引く。
- 陽子(2個):1.007276 Da × 2
- 中性子(2個):1.008665 Da × 2
- 電子(2個):0.000548 Da × 2
- 4He の原子質量(中性原子):4.002603 Da
結果を確認
うまいこと計算できましたか?
うまくいけばこういう結果が得られているはず。
- バラバラの合計質量 4.032978 Da
- 質量欠損 0.030375 Da
- 結合エネルギー 約28.30MeV
重水素との比較からわかること
重水素の結合エネルギーは約2.22MeV、それに対し4Heは約28.30MeV。
この数値をそれぞれの核子数(重水素なら2、4Heでは4)で除したものが「核子1個あたりの結合エネルギー」となります。
この核子1個あたりの結合エネルギーで両者を比較すると、重水素では1.11MeV、4Heでは7.1MeVとなり、4Heの方が強固に結合していることが分かりますね。
核子1個あたりの結合エネルギー
どっかで聞いたことあったような・・・


ちょっと前にやったじゃないか~。
ここだよ。
A15:原子核の質量が軽くなる?質量欠損とエネルギー
実際の問題を見ていきましょう。
ちょっと古い問題ですがご紹介していきましょう。
年代的に u で出題されていた時代ですので、 Da に置き換えています。
したがって、「改」の文字が付いています。
第51回 1999年 問14改
陽子、中性子および電子の質量をそれぞれ 1.0073Da 、 1.0087Da 、および 0.0005Da とする場合、 ${}^{12}\mathrm{C}$ の質量欠損 [Da] はどれか。
- 0.0059
- 0.059
- 0.099
- 0.59
- 0.99
いかがでしょうか?
国試の問題自体はここまでですが、続きとして、12Cの質量欠損をエネルギーに換算した場合は何MeVになるかも求めてみましょう。
定義をしっかりと覚えていれば、12Cの統一原子質量は分かりますよね?
当然12Daでしたよね。
もう一つ、1Daをエネルギーに換算すると931.5MeVでしたね。
うっかり忘れてしまった方は「A14:統一原子質量単位(ダルトン)とは?覚えるべき数値と使い方を解説」をCheckです。

解答を確認する。
答えは 3 です。
それをエネルギーに換算すると、 92.22MeV となります。
解説
陽子、中性子、電子の質量を足します。
$1.0073+1.0087+0.0005=2.0165 \mathrm{Da}$
それぞれ6個ずつありますから、質量の合計は
$2.0165×6=12.099 \mathrm{Da}$
12Cの質量は定義から12Daと決まっていますので、その質量欠損⊿Mは
$⊿M=12.099-12=0.099 \mathrm{Da}$ となります。
よって、答えは選択肢 3 ですね。
続きとして・・・
0.099DaをエネルギーEに換算するには931.5を乗じます。
$E=0.99×931.5=92.22 \mathrm{MeV}$ という具合になります。
医療現場でこの知識がどう役立つの?
医療現場でももちろん起きている現象なんですが、イメージしにくいので、今回は太陽の核融合のお話をご紹介。
太陽が輝いている理由も結合エネルギー
実は、太陽の中心では水素が融合してヘリウムになる「核融合」が絶えず起こっています。
このとき、水素4個を合わせた質量と、できあがったヘリウム1個の質量を比べると……やっぱり少し足りません。
その“消えた分”が莫大なエネルギーとなって放出され、光や熱となって地球に届いているのです。
つまり、私たちが毎日浴びている太陽の光も、もとはといえば原子核の結合エネルギー。
結合エネルギーを理解することは、「なぜ太陽が輝き続けられるのか」を知ることでもあったんですね。
まとめ
質量欠損と結合エネルギーは、言葉だけで聞くと難しく感じがちですが、
実際に数値を入れて計算してみると、その意味がはっきり見えてきます。
重水素で手順を確認し、4Heで練習し、12Cで国家試験レベルを体験することで、
「どう計算するのか」「どこを見ればいいのか」という型が身についたはずです。
あとは同じ流れを繰り返すだけ。計算は、慣れれば必ずできるようになります。

計算の流れさえつかめば、質量の差から結合エネルギーを出すのは意外と簡単なんだよ。
あとは自分で練習して慣れていこう!
お願い
本サイトに掲載されている図やイラストの著作権は管理人にあります。
無断掲載や転載はお断りさせていただきます。
また、リンクフリーではありますが、画像などへの直リンクはお控えください。
次に読むならコレ!電爺的おすすめ内部リンク

ほれ、ここまで読んだんなら、次はこのあたりを見ておくとえぇぞい。
次に読むならコレ!たまのすけおすすめ外部リンク

ここまで読んできた皆さんなら、もう一歩踏み込んだ知識に触れてみたくなるはずです。そんな方におすすめの外部リンクを紹介しますね。



コメント