「結合エネルギー」という言葉は知っていても、グラフになると「結局どこを見ればいいの?」って戸惑うことありますよね。
ここでは、結合エネルギーのグラフの“形”を読み解くことで、原子核の安定性がどう決まるのか見ていきましょう。
質量数の増加に伴う変化や、鉄(Fe)あたりで最大になる理由、そしてそれ以降に減少する原因まで、一つひとつ整理して確認していきましょう。
前回(A15)で学んだ「質量欠損と結合エネルギー」の考え方を土台にすれば、グラフの意味も自然と理解できるはずです。
グラフで見る核子1個あたりの結合エネルギー
A15:原子核の質量が軽くなる?質量欠損とエネルギーで触れたグラフを紐解いていきましょう。
まだA15をご覧になっていない方はそちらを先にチェックしていただくと理解がスムーズです。

核子1個あたりの結合エネルギー

横軸に質量数、縦軸に核子1個あたりの結合エネルギーをとったグラフを見ていきましょう。
と、その前に「核子1個あたりの結合エネルギー」の意味は分かりますか?
例えば、質量数4の原子核を例にとって考えてみます。
この原子核の結合エネルギーの合計が10MeVだとしましょう。
核子の数は質量数と同じですから4つです。
10MeVを4つで分け合うと考えればOKです。
つまり、この場合の核子1個あたりの結合エネルギーは2.5MeVとなります。
閑話休題(話を戻しまして)。
核子1個あたりのエネルギーは上のグラフのような変化を辿ります。
比例のような一辺倒な変化ではなく、複雑に変化しています。
この不規則に見える変化の特徴を見出していきます。
- 質量数の小さなところでは、質量数の増加とともに急激に結合エネルギーが上昇する。
- 質量数12以降では平均8MeVになる。
- 質量数56で最大8.8MeVになる。
- 質量数56以降は徐々に減少する。
- 偶々核の4He、12C、16Oはその他に比べて結合エネルギーが少し大きい。
質量数の小さなところでは、質量数の増加とともに急激に結合エネルギーが上昇する。

図の赤〇の部分のお話。
この領域では、質量数が大きくなるにつれ、核子1個あたりの結合エネルギーは急激に大きくなります。(グラフの立ち上がりが急峻になります。)
これは 表面効果 が原因です。
表面効果は後ほど説明します。
質量数12以降では平均8MeVになる。

図の青〇の部分のお話。
この領域では核子1個あたりの結合エネルギーの平均値が 8.0MeV になります。
※図は管理人の自作図です。キチンと測って平均値など出さないで下さいね。多少のズレはご愛嬌ってことで。
質量数56で最大8.8MeVになる。

質量数が約60(厳密には56Fe)のところで核子1個あたりの結合エネルギーの最大値が 8.8MeV になります。
平均値と値が近いので、間違えないようにしてください。出てくる数字は「8」ばっかりです。
質量数56以降は徐々に減少する。

図の緑〇の部分のお話。
56Feを境に徐々に減少していきます。
ここは クーロン効果 が働きます。
質量数が増えるということは、陽子の数も増え、クーロン斥力も増加してしまいます。
斥力は結合とは逆の属性になりますので、核子1個あたりの結合エネルギーは減少してしまいます。
偶々核の4He、12C、16Oはその他に比べて結合エネルギーが少し大きい。

図の紫〇の部分のお話。
低原子番号(低質量数)の核種の場合、陽子数と中性子数の等しい原子核は他のものよりちょっとだけ強く結合します。
グラフはノコギリの歯のようにギザギザします。
表面効果

質量数の小さな核種(図の左側)では原子核の表面になる割合が高くなり、結合エネルギーが小さくなります。
図の場合、4つの核子のうち4つすべてが表面にきています。
質量数の大きな核種(図の右側)では中央に存在する核子が出てきます。
図の場合、7つの核子のうち1つが中央で6つが表面更にる感じです。
質量数が更に大きくなれば、中央になる割合が増えていきます。
左の場合、表面の核子はその他2つと結合しています。
それに対し右の場合、中央の核子はその他6つと結合しています。
中央の核子の方が結合数が多いので、結合エネルギーの総合値が高くなります。
逆に言えば、表面になると結合エネルギーが小さくなります。
まとめると、質量数が小さい核種は表面になってしまう核子の割合が高くなり、結合エネルギーが小さくなります。
<補足>
表面張力は表面積に比例します。つまり質量数の2/3乗に比例します。
体積効果
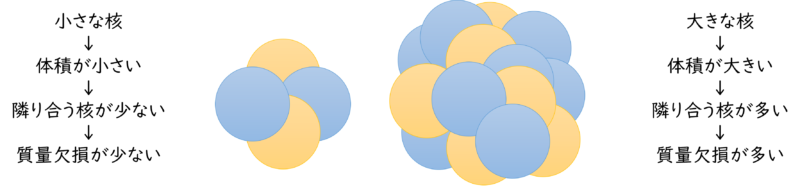
体積効果とは、質量欠損が体積に比例して大きくなる ことで生じる効果です。
核が大きくなるほど、核子(陽子+中性子)の数も増えていきます。
核子数は体積に比例するため、
核子どうしがつくる結びつきの総量(=質量欠損)が体積の増加に合わせて増える
というのが体積効果の基本的な考え方です。
これはイメージしやすいで。
オレでも分かるわ!

もう少しイメージで補足すると
核力(強い相互作用)は短い距離でしか働きませんが、
体積の中心にいる核子は周囲に多くの仲間がいるため、たくさんの結びつきが可能です。
- 小さな核 ⇒ 中心部が少なく、結びつける相手が限られる
- 大きな核 ⇒ 中心部が増え、結びつきの数が増える
つまり、
①質量欠損は体積に比例する
②核子数(質量数)が体積に比例するため
という関係が自然と成り立つわけです。
クーロン効果
原子核の中では陽子と中性子がぎゅっと集まっていますが、陽子どうしはどちらも正の電荷をもつため、クーロン力(静電気の反発力)が働きます。

この力は核を安定化させる方向ではなく、むしろ結合を弱める方向にはたらくというのがポイントです。
反発の大きさは、陽子の数が増えるほど大きくなります。
その増え方は単純な比例ではなく、陽子数の2乗に比例して急激に増えるという性質を持っています。
また、陽子どうしの距離が近いほどクーロン力は強くなるため、原子核の大きさ(体積の1/3乗=半径)によって反発の強さが変わってきます。
ここまでをまとめると、
- 陽子間にはクーロン力が働く
- クーロン力は結合を弱める方向にはたらく
- クーロン力は陽子数の2乗に比例する
- 陽子の距離(体積の1/3乗)に反比例して強さが変わる
というイメージになります。
また、クーロン効果が特に大きな影響を与えるのは重い原子核です。
陽子数が多いほど反発が急激に強まるため、強い相互作用(核力)だけでは安定を保ちきれなくなります。
その結果として、
- 重い元素は不安定になりやすい
- α壊変や自発核分裂を起こしやすい
- 鉄より重くなると結合エネルギーが下がる
といった現象が出てきます。
対称効果
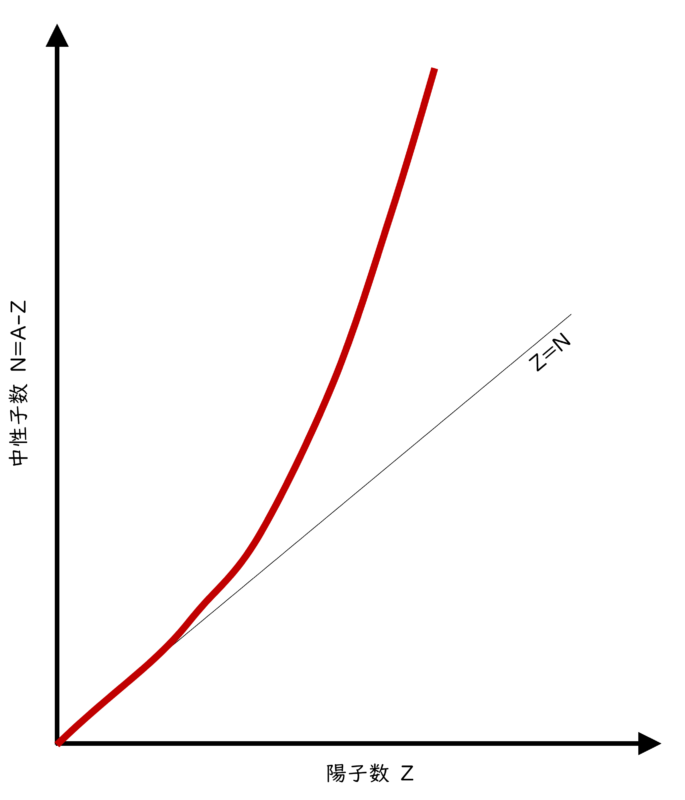
原子核の中では、陽子と中性子の数の“バランス”が、結合の強さに大きく影響します。
この「どんな比率だと安定するのか」を説明するのが 対称効果 です。
上のグラフでは安定な原子核は赤線のような関係性で分布しています。

陽子と中性子の“ちょうどいい比率”が核の安定をつくるんです。
低い原子番号の核では「陽子数=中性子数」が最も安定する
軽い核(⁴He、¹²Cなど)では、
陽子の数と中性子の数がほぼ等しいときに、もっとも強く結合します。
グラフでも、グラフの左側(低原子番号領域)では赤線がZ=Nのラインに乗っていますよね。
これは、核力の働きが陽子にも中性子にもほぼ同じで、
ちょうど1対1で組むとエネルギー的に安定しやすくなるためです。
- 陽子 = 中性子 → 結合が強い → 安定しやすい
重い核では中性子が多く必要になる
一方、鉄より重い元素では状況が変わります。
陽子が増えると、
陽子どうしのクーロン斥力 がどんどん強くなります。
クーロン斥力による反発が強くなるほど、
陽子と同じ数の中性子を入れただけでは核がまとまりにくくなります。
そのため、重い核では…
- 中性子数 > 陽子数
のほうが安定します。
グラフでは右側の高原子番号領域では、赤線はZ=Nのラインより上方にズレていっていますね。
これは、高原子番号だと中性子数の方が多くないと安定しないということになります。
これによって、鉄以降の重元素では
「陽子より中性子が多い」という特徴が現れます。
どうして、中性子が多い方が安定するんですか?


良いところに気付いたの。

中性子はクーロン斥力を発生させずに、結合するための核力だけを増やすことができるからだよ。
安定比は原子番号によって変化する
- 軽い核:
陽子:中性子 = 1:1 が安定 - 中程度の核(鉄付近):
中性子がやや多め - 重い核(ウランなど):
陽子:中性子 = 1:1.5 以上になることも
つまり、
原子番号が大きくなるほど、中性子多めでないと安定できない
というのが対称効果の本質です。
オレの体重が中性脂肪多めじゃないと維持できないのと一緒やな。


自虐ネタに磨きがかかってきたの~
奇数偶数効果
陽子と中性子には、それぞれが「ペア」をつくる性質があります。
そのため、陽子数と中性子数が偶数の核ほど安定しやすく、どちらかが奇数になると安定性は少し下がります。これは、粒子同士がペアをつくるとエネルギー的に有利になるためです。
その結果として、安定な原子核はおおまかに次の順で数が多くなります。
- 偶偶核(陽子・中性子とも偶数)
- 奇偶核(どちらか片方が奇数)
- 奇奇核(陽子・中性子とも奇数)
実際、奇奇核で安定したものは非常に少なく、ごく限られた4種類ほどしか存在しません。
例としては、²₁H、⁶₃Li、¹⁰₅B、¹⁴₇N などがあります。
こうした稀な核種は、陽子と中性子のペアがつくりづらいため、他と比べて安定性が低くなるのが特徴です。
奇々核の安定した核種って覚えた方がえぇんか?


簡単だよ。
原子番号を奇数を小さい順に並べる。
質量数は原子番号の倍にするだけだよ。
メチャクチャ簡単やんか!

結局どこを覚えればよいの?
結合エネルギーの詳細を説明するモデル(液滴模型など)では、
- 体積効果
- 表面効果
- クーロン効果
- 対称効果
といった項目が含まれます。
ただし国家試験で問われるのはグラフの大まかな特徴、
すなわち「鉄付近で最大」「それ以降は徐々に減少」という流れを押さえておけば十分です。
実際の問題を見ていきましょう。
と思いましたが、残念ながらドンピシャで該当するような出題はA15:原子核の質量が軽くなる?質量欠損とエネルギーで既に紹介してしまいました。
少し古いですが、選択肢の1つとして登場した問題をご紹介します。
第66回 2014年 問43
原子核について誤っているものはどれか。
- 核子は強い相互作用で結合している。
- 直径はおよそ10-15~10-14mである。
- 中間子はクォークと反クォークで構成されている。
- 1核子あたりの結合エネルギーはおよそ20MeVである。
- 中性子はアップクォーク1個とダウンクォーク2個で構成されている。
解答を確認する。
正解は 4 です。
各選択肢の考え方は以下の通り。
- 正しい。 核子(陽子・中性子)は強い相互作用で結合しているんでしたよね。その強い相互作用の名称は「核力」です。
- 正しい。 原子核の直径はおおよそ1~10 fm(10-15〜10-14 m)。半径は 質量数の1/3乗に比例するんでしたよね。
- 正しい。 中間子(メソン)=クォーク+反クォーク。
- 誤り。 核子1個あたりの結合エネルギーは約8 MeV、鉄で最大8.8 MeV。
- 正しい。 中性子 = u d d(アップ1、ダウン2)。ちなみに陽子は u u d (アップ2、ダウン1)でしたね。
医療現場でこの知識がどう役立つの?
結合エネルギーは、核が安定か不安定かを見極める基礎知識です。放射線技師の実務では、特に核医学で重要になります。
- アイソトープが放射線を出す理由
安定していない原子核(結合エネルギーのバランスが悪い核)は、より安定になるために壊変して放射線を放出します。これが核医学で利用する放射性同位元素(RI)です。 - 具体的な検査での例
SPECTでよく使う 99mTc は、余分なエネルギーをガンマ線として放出することで安定に近づきます。
PETで使う 18F は、陽電子を放出してより安定な核へ変わります。いずれも「結合エネルギーが不安定だから崩壊する」現象を利用しているんです。 - 実務でのつながり
核の安定性を理解していれば、「どの核種が壊変するか」「半減期がどのくらいか」「放出する放射線の種類は何か」が自然とイメージできるようになります。これはアイソトープ投与後の撮像計画や線量管理に直結する知識です。
つまり、結合エネルギーの理解=核が安定かどうかを判断する目につながり、核医学検査でRIを正しく安全に扱うための基礎になります。
まとめ
核子1個あたりの結合エネルギーのグラフを見ると、原子核の安定性が「質量数」によってどのように変化するかがよく分かります。
質量数が小さい領域では、質量数の増加とともに結合エネルギーが急激に増加し、鉄付近で最大となった後は、重くなるにつれて徐々に低下していきます。
この形は、核の安定性が一様ではないことを示しています。
その背景には、
体積効果による結合の増加、
表面効果による結合の弱まり、
クーロン効果による陽子間反発、
対称効果による陽子と中性子の比率、
そして 奇数偶数効果(対形成効果) といった、複数の要因が関わっています。
結合エネルギーのグラフは、これらの効果が重なり合った結果として現れているものです。
この関係を理解しておくことで、「どの核が安定しやすいか」「なぜ壊変が起こるのか」といった判断が、感覚ではなく理屈でできるようになります。

鉄で最大8.8MeV、以降は減少、平均8MeV――この流れを押さえておけば試験は安心です。核医学とのつながりも意識して覚えておきましょう。
漫言放語(まんげんほうご)

牛助、なんで机にご飯粒いっぱいつけてるの?

ほら見てみぃ。
バラバラの米粒はこぼれやすいけど、ギュッと握ったらおにぎり!
もうこぼれへんて。
これが結合エネルギーや!
うっまそうやろ~


安定したのはお腹のようじゃの・・・

相変わらず物凄い食い意地だね。
まぁ、核子も同じで、まとまるほど安定するんだ。
お願い
本サイトに掲載されている図やイラストの著作権は管理人にあります。
無断掲載や転載はお断りさせていただきます。
また、リンクフリーではありますが、画像などへの直リンクはお控えください。
次に読むならコレ!電爺的おすすめ内部リンク

ほれ、ここまで読んだんなら、次はこのあたりを見ておくとえぇぞい。
次に読むならコレ!たまのすけおすすめ外部リンク

ここまで読んできた皆さんなら、もう一歩踏み込んだ知識に触れてみたくなるはずです。そんな方におすすめの外部リンクを紹介しますね。



コメント